Математика
2.1.8. Простейшие системы уравнений с двумя неизвестными
Рейтинг: 0
Системы алгебраических уравнений
Множество уравнений, для которых требуется найти значения неизвестных, удовлетворяющие одновременно всем уравнениям, называется системой уравнений.
При решении системы уравнений применяются различные методы:
- метод исключения неизвестных,
- метод замены переменных,
- метод подстановки.
Пример 1. Решить систему уравнений:
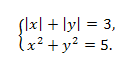
Решение. Решаем систему методом подстановки:
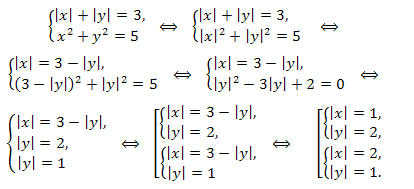
Заметим, что если \((x_0;y_0)\) – решение системы уравнений, тогда:
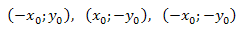 - тоже ее решения.
- тоже ее решения.
Пусть \(x,y\geq0\), тогда:
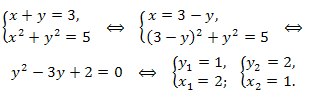
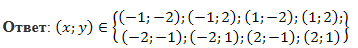
Пример 2. Решить систему уравнений:
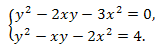
Решение.
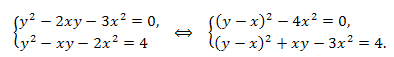
Вычтем из первого уравнения второе, получим равносильную систему:
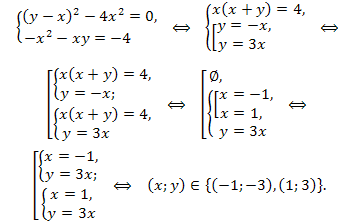

Время на изучение: 15 минут
Другие материалы по данной теме
Видео
Системы линейных уравнений с двумя неизвестными. Исследование систем
Определение
Система уравнений
