Для характеристики быстроты и направления движения вводится векторная величина – скорость.

Пусть материальная точка в момент времени t находилась в положении А, её положение определяется радиусом-вектором \(\vec r\)(t).

При движении в течение малого промежутка времени \(\Delta t\) точка пройдет по траектории путь \(\Delta S\) и получит элементарное перемещение \(\vec r\) (рис. 1.4).

Средней скоростью перемещения \(\left\langle {\vec v} \right\rangle \) называется отношение приращения \(\Delta \vec r\) радиуса-вектора точки к промежутку времени \(\Delta t\):

\(\left\langle {\vec v} \right\rangle = \frac{{\Delta \vec r}}{{\Delta t}}\). (1.8)

Направление вектора средней скорости совпадает с направлением \(\Delta \vec r\).

Вектор средней скорости – отношение перемещения к промежутку времени:

\(\begin{array}{l}\left\langle {{{\vec v}_{\rm{1}}}} \right\rangle = \frac{{\Delta {{\vec r}_1}}}{{\Delta {t_1}}};\begin{array}{*{20}{c}}{}&{\left\langle {{{\vec v}_{\rm{2}}}} \right\rangle = \frac{{\Delta {{\vec r}_2}}}{{\Delta {t_2}}};}\end{array}\\\left\langle {\vec v} \right\rangle = \frac{{\Delta \vec r}}{{\Delta t}};\quad \quad \left\langle v \right\rangle \uparrow \uparrow \Delta \vec r.\end{array}\) (1.9)

Вектор средней скорости характеризует изменение положения радиуса-вектора (рис. 1.5).

Материальная точка движется по криволинейной траектории.

За время \(\Delta {t_1}\) точка проходит путь \(\Delta {S_1}\) и получает приращение \(\Delta {\vec r_1}\), за время \(\Delta {t_2}\) – приращение \(\Delta {\vec r_2}\).

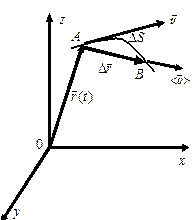
Рис. 1.4

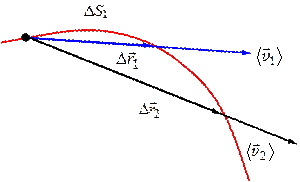
Рис. 1.5