Пример 1.

В каких точках графика функции \(f(x)=\frac{x}{x^2+1}\) касательная к нему параллельна оси абсцисс?

Решение:

Так как касательная параллельна оси абсцисс, то ее угловой коэффициент k = 0. Следовательно, f'(x)=0 в абсциссах точек касания. Найдем производную функции:

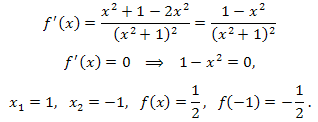
Таким образом, искомые точки графика: \(M(1;\frac{1}{2}),N(-1;-\frac{1}{2}).\)

Пример 2.

На рисунке 2 изображена прямая, являющаяся касательной к графику функции y=f(x) в точке (x₀;f(x₀)). Найдите значение производной в точке x₀.

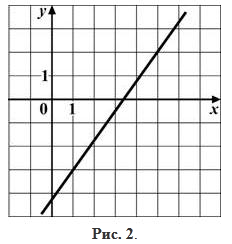
Решение:

По формуле \(f'(x_0)=tg\alpha,\) где α — угол наклона касательной к оси абсцисс, т.е.:

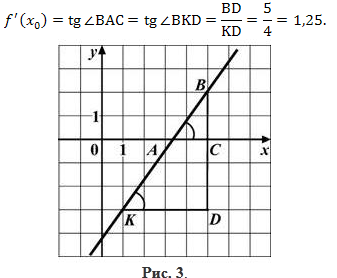
Примечание: В решении угол BAC был заменен на равный ему угол BKD, так как длины катетов треугольника ABC невозможно точно найти по рисунку в отличие от катетов треугольника KBD.

Пример 3.

Найдите уравнение касательной к графику функции \(f(x)=2^{x^2-4x}-1\) в точке ее пересечения с осью ОХ.
Решение: Абсциссы точек пересечения графика данной функции с осью OX находим из условия:

\(2^{x^2-4x}-1=0.\)

Отсюда следует:

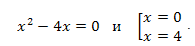
Уравнения касательных записываем по формуле:

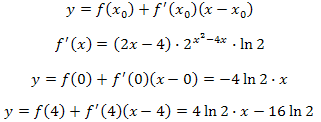
Пример 4.

К графику функции y=f(x), заданной на отрезке [–8; 7], проведена касательная в точке с абсциссой x₀ (рис. 4). Определите значение выражения x₀+f(x₀), если на рисунке изображены эта касательная и график производной данной функции.

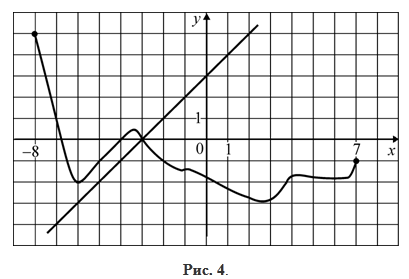
Решение. Из геометрического смысла производной следует \(f'(x_0)=k_{kac}.\). По рисунку видно, что касательной является прямая с угловым коэффициентом k = 1. Таким образом, \(f'(x_0)=1.\). По графику производной из условия \(f'(x_0)=1.\) находим \(x_0=-7.\). Учитывая, что в точке с абсциссой x₀ касательная соприкасается с графиком функции, имеем:

\(f(x_0)=y_{kac}(-7)=-4.\)

Тогда:

\(x_0+f(x_0)=-7-4=-11.\)