Существование производной функции f(x) в точке x₀ равносильно существованию невертикальной касательной в точке (x₀;f(x₀)) графика, при этом угловой коэффициент касательной равен f'(x₀) (рис. 1). В этом состоит геометрический смысл производной.

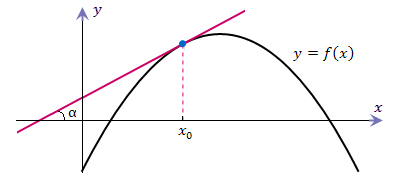
Кроме того, угловой коэффициент прямой равен тангенсу угла, образованного этой прямой с положительным направлением оси абсцисс. Таким образом, справедливо равенство:

\(f'(x_0)=k_{kac}=tg\alpha.\)

Уравнение касательной к графику функции y=f(x) в точке с абсциссой x₀:

\(y=f(x_0)+f'(x_0)(x-x_0).\)

Пример:

Найдите тангенс угла наклона касательной, проведенной к графику функции \(f(x)=2x-\frac{3}{x}\) в точке с абсциссой \(x_0=-1.\).
Решение. Применим ранее выписанную формулу \(tg\alpha=f'(x_0),\) где α — угол наклона касательной к оси абсцисс, а x₀— абсцисса точки касания. Так как:

\(f'(x)=2+\frac{3}{x^2},\)

то \(f'(-1)=2+3=5.\). Следовательно, \(tg\alpha=5.\)