Пусть функция \(f(x)\) определена в окрестности точки \(x_0\) , т.е. на некотором интервале, содержащем точку \(x_0\), и пусть точка \(x_0+\bigtriangleup x\) также принадлежит этому интервалу. Рассмотрим приращение функции \(f(x_0+\bigtriangleup x)-f(x_0)\) и составим отношение:

\(\frac{f(x_0+\bigtriangleup x)-f(x_0)}{\bigtriangleup x}.\)

Если существует предел этого отношения при \(\bigtriangleup x \rightarrow 0,\), то этот предел называется производной функции \(f(x)\) в точке \(x_0\) и обозначается \(f'(x_0):\)

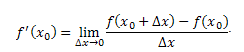
Приведем пример вычисления производной функции f(x) по определению. Пусть \(f(x)=3x-x^2,\) тогда:

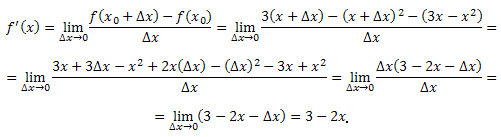
Таким образом: \((3x-x^2)'=3-2x.\)