Натуральное число называется простым, если оно имеет только два натуральных делителя: 1 и само себя.
Натуральное число, имеющее более двух натуральных делителей, называется составным. Заметим, что число 1 не относится ни к простым, ни к составным числам.
Евклид доказал, что множество простых чисел бесконечно.

Теорема. Всякое натуральное число n может быть представлено единственным образом в виде произведения простых множителей:

\(n=p^{k1}_1 \cdot p^{k2}_2 \cdot ... \cdot p^{kn}_n.\)

При разложении натурального числа на простые множители используют признаки делимости. При этом применяется запись столбиком: делимое слева от вертикальной черты, делитель справа, частное под делимым.
Пример представления составного числа в виде произведения простых множителей.

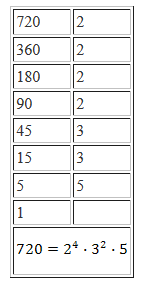
Примеры простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, ...