При решении многих задач требуется ответить на вопрос о делимости числа m на число n, не производя операции деления. Для этого используют признаки делимости. Опишем некоторые из них.
Делимость суммы. Если каждое из двух чисел a и b делится нацело на число с, то их сумма (разность) делится нацело на число с.

В самом деле, если a кратно с, то:

\(a=c\cdot n.\)

Если b кратно с, то:

\(b=c\cdot m.\)

Тогда:

\(a+b=c \cdot n+c\cdot m=c(n+m),\)

что означает кратность числа a + b числу с.
 Обратное не всегда верно. Например, числа 1 и 3 не кратны 2, а их сумма 1 + 3 = 4 кратна 2.

Делимость произведения. Если хотя бы один из сомножителей a, b делится нацело на число с, то произведение ab делится нацело на число с.
Пусть, например, a кратно с, то есть \(a=c\cdot n.\) Тогда:

\(ab=(cn)\cdot b=c\cdot(nb),\) 

что означает кратность произведения ab числу с.
 Обратное утверждение не всегда верно. Например, произведение \(ab=(cn)\cdot b=c\cdot(nb),\) кратно 6, хотя ни один из этих сомножителей 3 и 4 не кратен 6.

Признак делимости на 2. Натуральное число n делится на 2 тогда и только тогда, когда его последняя цифра делится на 2.
Пусть число k делится на 2. Представим его в десятичной системе счисления в виде:

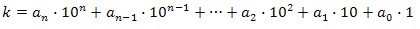
или в виде:

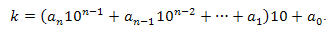
Число \((a_n10^{n-1}+a_{n-1}10^{n-2}+...+a_1)10\) делится на 2. Так как число k делится на 2 по условию, тогда разность этих чисел \(k-(a_n10^{n-1}+a_{n-1}10^{n-2}+...+a_1)10=a_0\)

также делится на 2 по признаку делимости разности.
 Обратно. Если \(a_0\) делится на 2, то \((a_n10^{n-1}+a_{n-1}10^{n-2}+...+a_1)10+a_0=k\) также делится на 2 по признаку делимости суммы.
 Аналогично можно доказать следующие признаки:

Признаки делимости на 3 и на 9. Натуральное число n делится на 3 (на 9) тогда и только тогда, когда сумма его цифр делится нацело на 3 (на 9).
Признак делимости на 5. Натуральное число n делится на 5 тогда и только тогда, когда последняя цифра в его записи 0 или 5.
Признаки делимости на 10, 100, 1000. Натуральное число n делится на 10 тогда и только тогда, когда последняя цифра в записи этого числа есть 0; на 100 – две последние цифры в записи этого числа – нули; на 1000 – три последние цифры – нули.
Признак делимости на 4. Натуральное число n делится на 4 тогда и только тогда, когда две его по-следние цифры или нули или образуют число, делящееся на 4.
Признак делимости на 8. Натуральное число n делится на 8 тогда и только тогда, когда три его по-следние цифры или нули или образуют число, делящееся на 8.
Признак делимости на 25. Натуральное число n делится на 25 тогда и только тогда, когда оно оканчи-вается на 00, 25, 50, 75.
Свойство последовательности натуральных чисел. Из n последовательных натуральных чисел:

\(a,a+1,a+2,...,a+(n-1)\)

одно и только одно делится на n.
 Пусть а – кратно n, т.е. a = nq, тогда утверждение верно.
 Пусть а не кратно n, тогда оно представлено в виде \(a=nq+r,\)

где \(r\in {1,2,...,n-1,}\) тогда число \(a+(n-r),\) находящееся среди данных чисел, делится нацело на n.
 В самом деле, \(a+(n-r)=nq+r+n-r=n(q+1).\)

Пример. Произведение чисел \((n-1)n(n+1)\) делится на 3 и делится на 2 и, значит, делится на 6.