Во множестве натуральных чисел всегда выполнимы операции сложения, умножения и возведения в степень. Не всегда выполнимы операции вычитания, деления и извлечения корня.
 Суммой двух натуральных чисел m и n называется натуральное число p, содержащее столько единиц, сколько их в m и n вместе. Операция нахождения суммы называется сложением. Записывается сложение следующим образом:

\(p=m+n.\)

Здесь p – сумма, а m и n - слагаемые.

Операция сложения обладает следующими свойствами:

1. \(m+n=n+m\) (перестановочность);

2. \((m+n)+p=m+(n+p)\) (сочетательное свойство).

Разностью двух натуральных чисел m и n называется натуральное число q такое, что:

\(m=n+q.\)

Записывается разность следующим образом:

\(q=m-n,\)

где числа m и n называются уменьшаемым и вычитаемым соответственно.
 Вычитание является операцией обратной по отношению к операции сложения, потому что позволяет по известной сумме двух слагаемых и одному из них найти другое слагаемое.
 Заметим, что операция вычитания не всегда выполнима во множестве натуральных чисел, например,

\(5-7=-2 \notin N.\)

Произведением натурального числа m на натуральное число n называется натуральное число k, равное сумме n чисел, каждое из которых равно m, т.е.

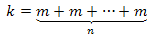
Операция нахождения произведения называется умножением и записывается следующим образом:

\(k=m \cdot n.\)

Здесь k – произведение, m и n – сомножители.
Умножение натуральных чисел обладает следующими свойствами:

1. \(m\cdot n = n \cdot m\)(перестановочность);

2. \((m\cdot n)\cdot p=m\cdot (n \cdot p)\) (сочетательное свойство).

Операции сложения и умножения чисел связаны распределительным законом:

\(m:n=\frac{m}{n}=a.\)

При этом m называется делимым, n – делителем, а – частным.
 Операция деления является обратной по отношению к операции умножения, так как позволяет по известным произведению и одному из сомножителей найти второй сомножитель.
 Заметим, что операция деления не всегда выполнима во множестве натуральных чисел, например,

\(15:4 \notin N.\)

Если при делении натурального числа m на натуральное число n частное есть также число натуральное, то говорят, что число m делится нацело на число n или что m – кратно n. Например, число 24 кратно каждому из чисел множества {1, 2, 3, 4, 6, 8, 12, 24}.

Все числа, кратные числу 2, называются четными, остальные – нечетными.
 Если число m не делится нацело на число n, то выполняют деление с остатком. Деление с остатком есть отыскание наибольшего натурального числа, которое при умножении на делитель дает число, не превышающее делимое. В этом случае записывают:

\(m=n\cdot p+r,\)

где r может принимать значения 1, 2, …, n – 1. При этом m называют делимым, n – делителем, p – неполным частным, r – остатком. Например,

\(14=3\cdot 4+2.\)