Пример 1. Решите неравенство:

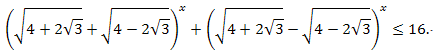
Решение:

Так как \(4+2\sqrt {3}=(\sqrt{3}+1)^2\), а также \(4-2\sqrt {3}=(\sqrt{3}-1)^2\), то данное неравенство можно записать в виде:

\((2\sqrt{3})^x+2^x \leq16.\)

Разделим обе части неравенства на \(2^x\) и исследуем полученное неравенство:

\((\sqrt{3})^x+1 \leq16\cdot2^{-x}.\)

Так как \((\sqrt{3})^x+1\) возрастает с увеличением \(x\), а \(16\cdot2^{-x}\) убывает, и равенство выполняется при x = 2, то при x < 2:

\((\sqrt{3})^x+1 <16\cdot2^{-x}.\)

Следовательно, решением исходного неравенства является множество x ≤ 2.

Ответ: \((-\infty;2].\)

Пример 2. Решите неравенство:

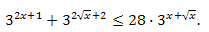
Решение:

Разделив обе части неравенства на \(3^{x+\sqrt{x}},\) получим:

\(3^{x-\sqrt{x}+1}+3^{-x+\sqrt{x}+2} \leq28.\)

Обозначим \(3^{x-\sqrt{x}}=t>0\) и запишем неравенство через переменную t:

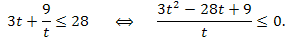
Так как t >0, то:

\(3t^2-28t+9\leq0,\)

\(\frac{1}{3}\leq t \leq9.\)

Возвращаясь к переменной x, получим:

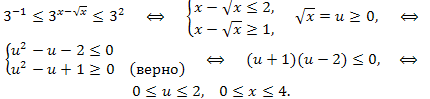
Ответ: \([0;4].\)

Пример 3. Решите неравенство:

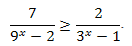
Решение:

Запишем цепочку равносильных переходов, в которой третий переход осуществлён в силу приведённой ранее теоремы 1:

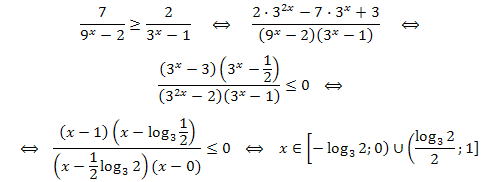
Ответ:
\((-\infty;-\frac{3}{5}]\cup[\frac{1}{2};+\infty).\)