Пример 1. Решите неравенство:

\((\sqrt{2}+1)^x+1<2(\sqrt{2}-1)^x.\)

Решение:

Заметим, что \(\sqrt{2}-1=\frac{1}{\sqrt{2}+1}.\) Поэтому:

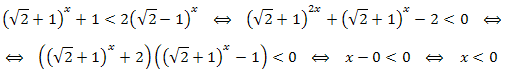
Ответ: \((-\infty;0).\)

Пример 2. Решите неравенство:

\(\LARGE 3^{(x+2)^2}+\frac{1}{27}\leq 3^{x^2-3}+9^{2x+2}.\)

Решение:

Преобразуем и воспользуемся теоремой 1:

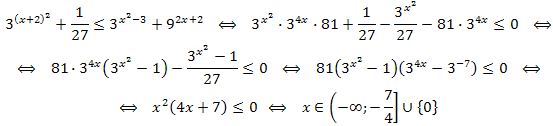
Ответ: \((-\infty;-\frac{7}{4}]\cup{{0}}.\)

Пример 2. Решите неравенство:

\(\LARGE |4^{3x}-2^{4x+2}\cdot 3^{x+1} +20 \cdot 12^x\cdot 3^x| \geq 8 \cdot 6^x\cdot (8^{x-1}+6^x).\)

Решение:

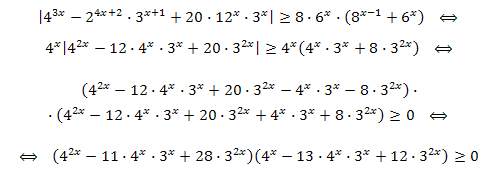
Разделим последнее неравенство на \(3^{4x}>0\) и сделаем замену переменной \(t=(\frac{4}{3})^x>0.\) Тогда неравенство примет вид:

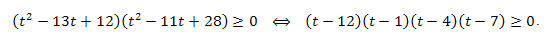
Возвратимся к старой переменной и для каждого множителя воспользуемся теоремой 1, учтя, что \((\frac{4}{3}-1)>0\):

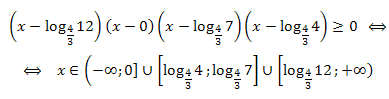
Ответ: \((-\infty;0]\cup[log_{\frac{4}{3}}4;log_{\frac{4}{3}}7]\cup[log_{\frac{4}{3}}12;+\infty).\)