Математика
2.1.5. Показательные уравнения
Показательные уравнения
При решении уравнений с показательными функциями
\(a^{f(x)}=a^{g(x)},a>0,\)
возможны два случая:
1. a = 1, f(x) и g(x) определены;
2. a > 0, a ≠ 1, f(x) = g(x).
При решении неравенств с показательными функциями
\(a^{f(x)}>a^{g(x)},a>0,\)
возможны три случая:
1. a > 1, f(x) > g(x).
2 a = 1, нет решений;
3. 0 < a < 1, f(x) < g(x).
Заметим, что в случае нестрогого неравенства между показательными функциями нестрогим становится и неравенство между функциями f(x) и g(x), причём случай a = 1 рассматривается отдельно.
Если в качестве основания степени выступает не число, а функция a(x), то эта ситуация требует особого внимания и имеют место следующие равносильные переходы:
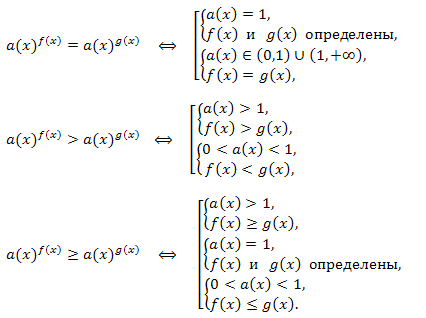
Требование a(x) > 0 следует из определения показательной функции.
Имеет место важная Теорема 1:
Знак разности \(a(x)^{f(x)}>a(x)^{g(x)}\) совпадает со знаком произведения \((a(x)-1)(f(x)-g(x))\) в области допустимых значений функций a(x) > 0, f(x), g(x).
Тогда условия равносильности можно записать в виде:
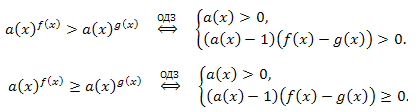
Замечание. Имеют место условия равносильности:
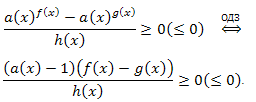
Другие материалы по данной теме
Видео
4.2. Показательные уравнения
