По определению модуля, число a имеет модуль:

\(|a| = \left\{ \begin{array}{l}a;a \ge 0;\\ - a;a < 0.\end{array} \right.\)

 Геометрически модуль числа есть расстояние от точки a на числовой прямой до начала координат.
 При решении уравнения, содержащего переменную под знаком обычно одного модуля, следует на основании определения модуля разбить область допустимых значений переменной на интервалы, на каждом из которых выражение, стоящее под знаком модуля, сохраняет знак.
 На каждом полученном интервале следует записать уравнение без знака модуля и решить его. Объединение множеств решений, найденных на рассматриваемых интервалах области допустимых значений переменной, составляет множество всех решений уравнения.

1. Уравнение \(f(|\phi(x)|)=g(x)\) по определению модуля равносильно совокупности систем:

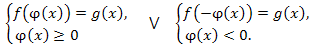
Пример.

Ответ: \(x=2;x=-1-\sqrt{5}.\)

2. Уравнения вида \(|f(x)|=g(x)\) можно решать двумя способами в зависимости от вида функций f(x) и g(x). По определению модуля уравнение \(|f(x)|=g(x)\) равносильно совокупности систем:

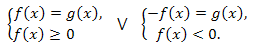
Пример.

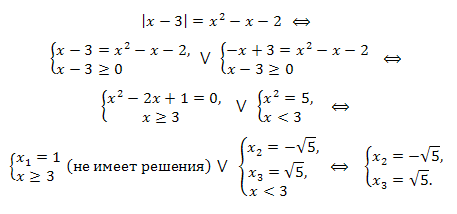
Ответ: \(x=\pm \sqrt{5}.\)

3. Уравнение \(|f(x)|=|g(x)|\) имеет смысл при условии \(g(x)\geq0,\) так как \(|f(x)|\geq0,\) поэтому имеем:

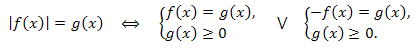
Пример.

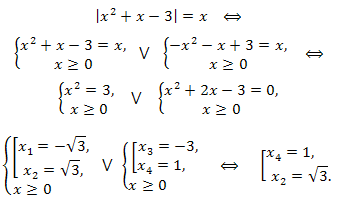
Ответ: \(x= \sqrt{3}; x=1.\)

4. Уравнение \(|f(x)|=|g(x)|\) равносильно совокупности уравнений :

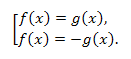
Пример.

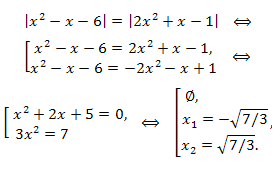
Ответ: \(x= \pm \sqrt{7/3}.\)