Если уравнение имеет вид:

\(|f_1(x)|+|f_2(x)|+...+|f_n(x)|=g(x),\)

т. е. содержит несколько модулей от функции одной переменной, то его удобно решать методом интервалов.
Сначала решаем уравнения:

\(f_1(x)=0;f_2(x)=0;...;f_n(x)=0,\)

т. е. находим точки, которые делят область допустимых значений переменной x на промежутки, на которых функции \(f_1(x),f_2(x),...,f_n(x)\) сохраняют знак. Затем, используя определение абсолютной величины, переходим от заданного уравнения к совокупности уравнений, полученных на каждом промежутке и не содержащих знак модуля, и решаем их.

Пример.

Решить уравнение:

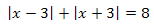
Решение. Находим точки, при переходе через которые выражения, стоящие под знаком модуля, меняют знак. Имеем две такие точки: x = 3 и x = –3. Таким образом, числовая прямая разбивается точками x = 3, x = –3 на промежутки знакопостоянства функций \(f_1(x)=x-3\) и \(f_2(x)=x+3\)

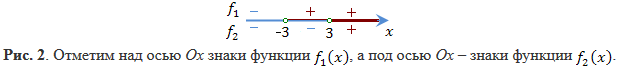
Решаем уравнение на каждом из промежутков:

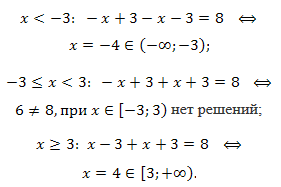
Объединяем найденные решения, получаем \(x_{1,2}=\pm 4.\)

Ответ: \(x_{1,2}=\pm 4.\)