Решить уравнение:

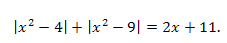
Решение. Применим метод интервалов. Находим нули функций \(f_1(x)=x^2-4\) и \(f_2(x)=x^2-9\) , решая уравнения:

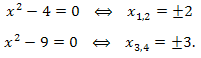
Определим знаки функций:

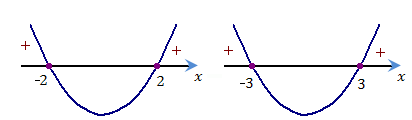
Нанесём знаки каждой из функций над и под числовой прямой:

Запишем уравнение на каждом промежутке без знака модуля и решим его. Получим:

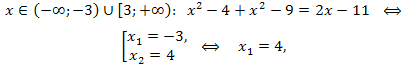
так как \(x=-3\notin(-\infty;-3);\)

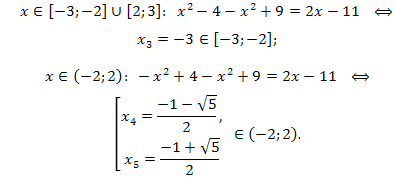
Ответ: \(x=4;x=-3;x=\frac{-1\pm \sqrt{5}}{2}.\)

Уравнение вида \(af^2(x)+b|f(x)|+c=0\) удобно решать заменой переменной \(|f(x)|=t\). Найдя неотрицательный корень уравнения \(t=t_0\), получаем два уравнения \(f(x)=\pm t_0\), решая которые, находим значение x.

Пример.

Решить уравнение:

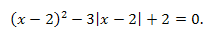
Решение. Сделав замену переменной \(|x-2|=t,\) где \(t\geq0,\) записываем и решаем уравнение:

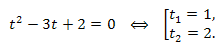
Возвращаясь к старой переменной, решаем два уравнения:

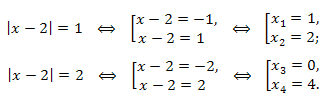
Ответ: \(x={0;1;3;4}.\)