Физика
1.1.8. Движение точки по окружности
Понятие о кривизне траектории
Если материальная точка движется по криволинейной траектории, то отличие этой траектории от прямолинейной траектории характеризуется радиусом кривизны, или кривизной траектории.
|
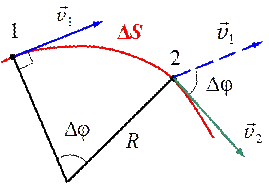
Рис. 1.8 | На рис. 1.8 Δφ – угол между касательными в точках, отстоящих друг от друга на расстоянии ΔS. Кривизна траектории \(C = \mathop {\lim }\limits_{\Delta S \to 0} \frac{{\Delta \phi }}{{\Delta S}} = \frac{{{\rm{d}}\phi }}{{{\rm{d}}S}}.\) (1.19) Кривизна траектории характеризует скорость поворота касательной при движении. |
Радиус кривизны траектории в данной точке есть величина, обратная кривизне:
\(R = \frac{1}{C}.\) (1.20)
Радиус кривизны траектории в данной точке – это радиус окружности, которая сливается на бесконечно малом участке в данном месте с кривой (рис. 1.8).
Другие материалы по данной теме
Формула
\(\vec \omega = \mathop {\lim }\limits_{\Delta t \to 0} \,\,\frac{{\Delta \vec \varphi }}{{\Delta t}}\)
Определение
Равномерное движение точки по окружности
Видео
Движение по окружности