Физика
1.1.8. Движение точки по окружности
Связь между линейными и угловыми характеристиками движения
Рассмотрим произвольную точку тела М, которая находится на расстоянии R от оси вращения и вращается с постоянной угловой скоростью \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \omega } \) (рис. 2.8). Пусть за время \(\Delta t\) тело повернулось на угол \(\Delta \phi \), а точка прошла путь \(\Delta S\).
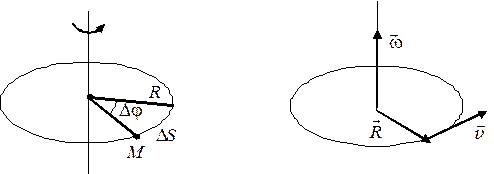
Рис. 2.8
Установим связь между линейными характеристиками точки (\(\Delta S,v,a\)) и угловыми характеристиками тела (\(\Delta \phi ,\omega ,\varepsilon \)). Длина пути \(\Delta S\) и угол поворота \(\Delta \phi \) связаны известным соотношением
\(\Delta S = R \cdot \Delta \phi \). (2.10)
Делим обе части равенства на \(\Delta t\) и переходим к пределу
\(\mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta S}}{{\Delta t}} = R\mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \phi }}{{\Delta t}}\). (2.11)
Отсюда имеем
\(v = \omega \). (2.12)
Формула (2.12) связывает модули линейной и угловой скоростей. Найдем выражение, связывающее векторы \(\vec v\) и \(\vec \omega \). Положение рассматриваемой точки тела будем определять с помощью вектора \(\vec R\), который проведен в данную точку тела перпендикулярно к оси вращения.
Тогда можем записать формулу для линейной скорости как векторное произведение:
\(\vec v = \left[ {\vec \omega \vec R} \right]\). (2.13)
При этом модуль векторного произведения, по определению, равен \(v = \omega R\sin (\vec \omega \hat R)\), а направление совпадает с направлением поступательного движения правого винта при его вращении от \(\vec \omega \) к \(\vec R\).
Пусть тело вращается неравномерно (рис. 2.9). Тангенциальное ускорение точки
\({a_\tau } = \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = R\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = R\varepsilon \). (2.14)
Векторы \({\vec a_\tau },\;\vec R,\;\vec \varepsilon \) взаимно перпендикулярны, поэтому можно записать, что
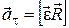 . (2.15)
. (2.15)
Модуль тангенциального ускорения \({a_\tau } = \varepsilon R\sin (\vec \varepsilon \ \vec R{\rm{)}}\).
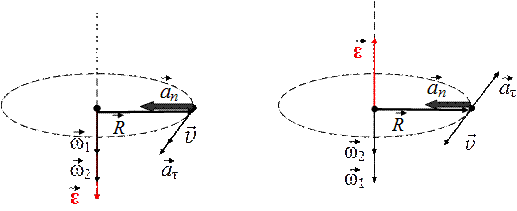
Рис. 2.9
Нормальное ускорение точки
\({a_n} = \frac{{{v^2}}}{R} = \frac{{{\omega ^2}{R^2}}}{R} = {\omega ^2}R\). (2.16)
Вектор нормального ускорения направлен по радиусу к центру окружности – против вектора \(\vec R\), тогда можно записать
\({\vec a_n} = - {\omega ^2}\vec R\). (2.17)
Формулы (2.14) и (2.16) связывают модули тангенциального и нормального ускорений точки с угловым ускорением \(\varepsilon \) и угловой скоростью \(\omega \) тела.
В заключение сопоставим формулы, которые связывают кинематические характеристики твердого тела (\(\phi ,\omega ,\varepsilon \)) с соответствующими формулами поступательного движения точки.
| Вид движения | Поступательное движение | Вращательное движение |
| Равномерное движение | \(v\) = const; S = \(v\)t | \(\begin{array}{l}\omega = {\rm{const;}}\\\phi = \omega t\end{array}\) |
| Равнопеременное | a = const; \(\begin{array}{l}v = {v_0} \pm at;\\S = {v_0}t \pm \frac{{a{t^2}}}{2}\end{array}\) | \(\begin{array}{l}\varepsilon = {\rm{const;}}\\\omega = {\omega _0} \pm \varepsilon t;\\\phi = {\omega _0}t \pm \frac{{\varepsilon {t^2}}}{2}\end{array}\) |
Другие материалы по данной теме
Определение
Равномерное движение точки по окружности
Формула
\(\vec \omega = \mathop {\lim }\limits_{\Delta t \to 0} \,\,\frac{{\Delta \vec \varphi }}{{\Delta t}}\)
Видео
Движение по окружности
