Физика
1.1.8. Движение точки по окружности
Тангенциальное ускорение
Составляющая ускорение \({\vec a_\tau }\) называется тангенциальным ускорением. Оно характеризует быстроту изменения скорости по величине. Его численное значение равно первой производной по времени от модуля скорости:
\({a_\tau } = \frac{{{\rm{d}}v}}{{{\rm{d}}t}}\). (1.23)
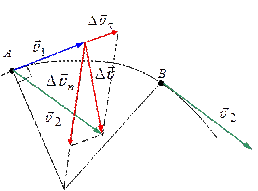
Определим направление вектора \({\vec a_\tau }\). При \(\Delta t \to 0\) направление вектора \(\Delta {\vec v_\tau }\) стремится к направлению вектора \(\vec v\) в точке А траектории. Значит, вектор \({\vec a_\tau }\) направлен по касательной к траектории (рис. 1.10).
|
Рис. 1.10 |
Из рис. 1.10 видим, что \(\begin{array}{l}\Delta \vec v = {{\vec v}_2} - {{\vec v}_1};\\\Delta \vec v = \Delta {{\vec v}_\tau } + \Delta {{\vec v}_n};\\{{\vec a}_\tau } \uparrow \uparrow \Delta {{\vec v}_\tau };\\{{\vec a}_n} \uparrow \uparrow \Delta {{\vec v}_n}.\end{array}\) (1.24)
|
Другие материалы по данной теме
Видео
Движение по окружности
Формула
\(\vec \omega = \mathop {\lim }\limits_{\Delta t \to 0} \,\,\frac{{\Delta \vec \varphi }}{{\Delta t}}\)
Определение
Равномерное движение точки по окружности