Составляющая ускорения \({\vec a_n}\) называется нормальным ускорением. Оно характеризует быстроту изменения скорости по направлению. Нормальное ускорение направлено по радиусу к центру кривизны траектории.

Найдем выражение для \({\vec a_n}\). Восстановим в точках А и В перпендикуляры к касательным. Они пересекутся в точке О. При \(\Delta t \to 0\) дугу АВ можно рассматривать как дугу окружности радиуса R. Из подобия треугольников CAE и AOB следует равенство отношений

\(\frac{{\Delta {v_n}}}{{{v_1}}} = \frac{{\Delta r}}{R}\); (1.25)

\({a_n} = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta {v_n}}}{{\Delta t}} = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{{v_1} \cdot \Delta r}}{{\Delta t \cdot R}} = \frac{{v_1^2}}{R}\). (1.26)

Итак, нормальное ускорение

\({a_n} = \frac{{{v^2}}}{R}\), (1.27)

где R – радиус кривизны траектории.

Радиус кривизны представляет собой радиус окружности, которая сливается в данном месте с кривой на бесконечно малом ее участке. Если траектория – окружность, то R – радиус этой окружности.

Определим направление вектора \({\vec a_n}\). При \(\Delta t \to 0\), угол \(\alpha \to 0\) и \(\Delta {\vec v_n}\) в пределе перпендикулярен \({\vec v_1}\), следовательно, \({\vec a_n} \bot {\vec v_1}\). Полное ускорение

\(a = \sqrt {a_\tau ^2 + a_n^2} = \sqrt {{{\left( {\frac{{{\rm{d}}v}}{{{\rm{d}}t}}} \right)}^2} + {{\left( {\frac{{{v^2}}}{R}} \right)}^2}} \). (1.28)

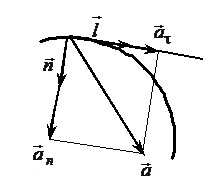
Пусть \(\vec l\) и \(\vec n\) – векторы единичной длины, один направлен вдоль скорости, а другой – перпендикулярно ему (рис. 1.11), при этом

\(\left| {\vec l} \right| = \left| {\vec n} \right| = 1\).

Тогда в векторном виде

\(\vec a_\tau ^{} = \frac{{{\rm{d}}v}}{{{\rm{d}}t}} \cdot \vec l\); \({\vec a_n} = \frac{{{v^2}}}{R} \cdot \vec n\); \(\vec a = \frac{{{\rm{d}}v}}{{{\rm{d}}t}} \cdot \vec l + \frac{{{v^2}}}{R} \cdot \vec n\). (1.29)