Пусть материальная точка движется по криволинейной траектории. Рассмотрим общий случай, когда скорость движения меняется по величине и направлению.

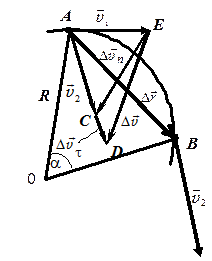
Рис. 1.9.

Пусть материальная точка в положении А имела скорость \({\vec v_1}\) (рис. 1.9). Через промежуток времени \(\Delta t\) точка перешла в положение В, где ее скорость оказалась равной \({\vec v_2}\).

Перенесем вектор \({\vec v_2}\) параллельно самому себе в точку А (вектор \(\mathop {AD}\limits^ \to \)) и найдем вектор \(\Delta \vec v\), равный \(\Delta \vec v = {\vec v_2} - {\vec v_1}\).

Так как в общем случае скорость может меняться по величине и направлению, то удобно разложить ускорение на две составляющие. Для этого разложим на две составляющие вектор \(\Delta \vec v\).

Из точки А по направлению скорости \({\vec v_2}\) отложим вектор \(\mathop {AС}\limits^ \to \), по модулю равный вектору \({\vec v_1}\). Очевидно, что вектор \(\mathop {CD}\limits^ \to \), равный \(\Delta {\vec v_\tau }\), характеризует изменение скорости по величине. Вектор \(\Delta {\vec v_n}\) характеризует изменение скорости по направлению

\(\Delta \vec v = \Delta {\vec v_\tau } + \Delta {\vec v_n}\). (1.21)

Полное ускорение

\(\begin{array}{l}\vec a = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \vec v}}{{\Delta t}} = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta {{\vec v}_\tau }}}{{\Delta t}} + \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta {{\vec v}_n}}}{{\Delta t}} = {{\vec a}_\tau } + {{\vec a}_n};\\\vec a = {{\vec a}_\tau } + {{\vec a}_n}.\end{array}\) (1.22)