Физика
1.4.3. Закон изменения и сохранения импульса
Закон сохранения момента импульса
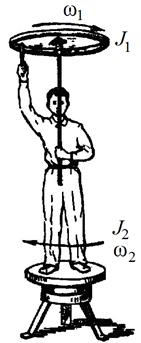
Пример 3. Человек стоит на неподвижной скамье Жуковского и держит в руках ось массивного колеса так, что она является продолжением оси ОО1 вращения скамьи (рис. 6.11).
| Вначале колесо не вращается, а затем человек раскручивает его до угловой скорости \({\vec \omega _1}\). При этом он сам вместе со скамьей приходит во вращение в обратном направлении с угловой скоростью \({\vec \omega _2}\), которая, как показывает опыт, находится в полном согласии с законом сохранения момента импульса системы относительно неподвижной оси ОО1: \(\vec L = {\rm{const}}\). Вначале скамья не вращается, поэтому суммарный момент импульса системы равен нулю: \(\vec L = 0\); после того как колесо раскрутили, суммарный момент импульса системы равен сумме моментов импульса колеса и скамьи: \(\vec L = {\vec L_{\rm{}}} + {\vec L_{{\rm{}}}} = {I_{\rm{}}}{\vec \omega _1} + {I_{{\rm{}}}}{\vec \omega _2} = 0\). Из этого уравнения следует, что \({\vec \omega _2} = - \frac{{{I_{\rm{}}}}}{{{I_{{\rm{}}}}}}{\vec \omega _1}\). Скамья вращается в противоположном направлении вращению колеса.
|
|
| Рис. 6.11 |
Пример 4. Рассмотрите внимательно рисунок и объясните явление (рис. 6.12).
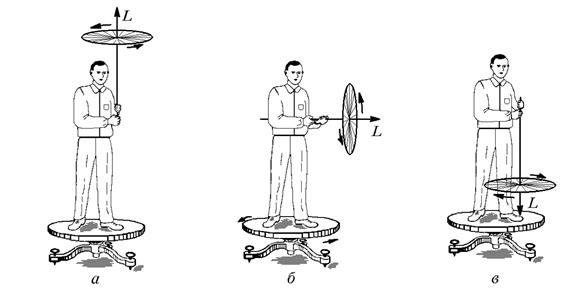
Рис. 6.12
Другие материалы по данной теме
Формула
\(\vec F = m{\vec a_{\rm{c}}}\)
Определение
Механическая система
Видео
2.10. Закон сохранения импульса