В любой системе частиц имеется одна замечательная точка С, называемая центром масс (или центром инерции), которая обладает рядом интересных свойств. Ее положение относительно начала О данной системы отсчета характеризуется радиусом-вектором 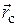, определяемым как

\({\vec r_{\rm{c}}} = \frac{1}{m}\sum\limits_{i = 1}^n {{m_i}{{\vec r}_i}} \), (6.5)

где \({m_i}\) и \({\vec r_i}\) – масса и радиус-вектор 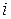-й частицы; m – масса всей системы; n – число частиц в системе.

Следует заметить, что центр масс системы совпадает с ее центром тяжести, впрочем, это утверждение справедливо лишь в том случае, когда поле сил тяжести в пределах данной системы можно считать однородным.

Найдем скорость \({\vec v_{\rm{c}}}\) центра масс системы:

\({\vec v_{\rm{c}}} = \frac{{{\rm{d}}{{\vec r}_{\rm{c}}}}}{{{\rm{d}}t}} = \frac{1}{m}\sum\limits_{i = 1}^n {{m_i}} {\vec v_i}\). (6.6)

Учитывая, что \({\vec P_i} = {m_i}{\vec v_i}\), а \(\sum\limits_{i = 1}^n {{{\vec P}_i}} \) – есть импульс \(\vec P\) системы, можно написать

\(\vec P = m{\vec v_{\rm{c}}}\), (6.7)

т.е. импульс системы равен произведению массы системы на скорость ее центра масс. Продифференцируем выражение (6.7) по времени:

\(\frac{{{\rm{d}}\vec P}}{{{\rm{d}}t}} = m\frac{{{\rm{d}}{{\vec v}_{\rm{c}}}}}{{{\rm{d}}t}}\).

По второму закону Ньютона \(\frac{{{\rm{d}}\vec P}}{{{\rm{d}}t}} = \vec F\), отсюда получаем

\(\vec F = m{\vec a_{\rm{c}}}\), (6.8)

где \({\vec a_{\rm{c}}}\) – ускорение центра масс системы; \(\vec F\) – геометрическая сумма внешних сил, приложенных к системе.

Это и есть уравнение движения центра масс системы: центр масс системы частиц движется так, как двигалась бы материальная точка, в которой сосредоточена масса всей системы под действием всех приложенных к системе внешних сил.

Пример 2. Человек прыгает с вышки в воду. Движение прыгуна в общем случае имеет весьма сложный характер. Однако если сопротивление воздуха пренебрежимо мало, то можно сразу утверждать, что центр масс прыгуна движется по параболе, как материальная точка, на которую действует постоянная сила \(m\vec g\), где m – масса человека.

Из уравнения (6.8) следует, что если внешние силы \(\vec F = 0\), то \({\vec a_{\rm{c}}} = 0\), т.е. центр масс системы либо движется равномерно и прямолинейно, либо остается неподвижным.

Уравнение (6.8) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на систему частиц.