Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему:

\(\frac{{{\rm{d}}\vec P}}{{{\rm{d}}t}} = {\vec F^{в\rm{}}}\). (6.3)

Полученное выражение представляет собой закон изменения импульса \(\vec P\) системы материальных точек и показывает, что скорость изменения импульса системы определяется только внешними силами.

Из этого уравнения следует, что приращение импульса системы равно импульсу внешних сил: \({\rm{d}}\vec P = {\vec F^{\rm{}}}{\rm{d}}t\) или \(\Delta \vec P = {\vec P_{к\rm{}}} - {\vec P_{н\rm{}}} = \int\limits_0^t {{{\vec F}^{в\rm{}}}{\rm{d}}t} \), где \({\vec P_{к\rm{}}}\) и \({\vec P_{н\rm{}}}\) – импульс системы в конечном и начальном состоянии соответственно.

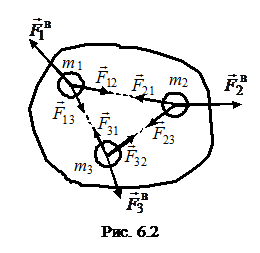
Рассмотрим замкнутую систему (внешние силы отсутствуют), рис. 6.2. Тогда

\(\frac{{{\rm{d}}\vec P}}{{{\rm{d}}t}} = 0\), (6.4)

т.е. \(\vec P = {\rm{const}}\).

Последнее выражение является законом сохранения импульса:
импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Отметим, что закон сохранения импульса выполняется и для незамкнутой системы, если геометрическая сумма всех внешних сил равна нулю.

Импульс системы материальных точек приблизительно сохраняется (не изменяется), если ограниченная по модулю внешняя сила действует в течение очень малого промежутка времени \(\Delta t\). Действительно, согласно уравнению \(\Delta \vec P = {\vec P_{к\rm{}}} - {\vec P_{н\rm{}}} = \int\limits_0^t {{{\vec F}^{в\rm{}}}{\rm{d}}t} \) приращение импульса за промежуток времени \(\Delta t\) равно \(\Delta \vec P = \int\limits_0^{\Delta t} {{{\vec F}^{в\rm{}}}{\rm{d}}t} = \vec F_{{ср\rm{}}}^{в\rm{}}\Delta t\), где \(\vec F_{{ср\rm{}}}^{в\rm{}}\) – средняя внешняя сила за промежуток времени \(\Delta t\).

Если время \(\Delta t\) мало, то \(\Delta \vec P \approx 0\) или \(\vec P = {\rm{const}}\), т.е. импульс приблизительно остается постоянным.

Пример 1. Во время взрыва в воздухе снаряда на него действует внешняя сила – сила тяжести. Время взрыва мало, поэтому импульсом силы тяжести можно пренебречь (не учитывать). Следовательно, импульс снаряда непосредственно перед взрывом равен суммарному импульсу образовавшихся осколков сразу после взрыва.

Для неограниченной по модулю внешней силы это утверждение несправедливо.

Закон сохранения импульса является фундаментальным законом природы. Он обладает большей общностью, чем законы классической механики (законы Ньютона).