Закон сохранения импульса является следствием второго и третьего законов Ньютона. Тела, входящие в систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими системе.

Механическая система – совокупность материальных точек (тел), рассматриваемых как единое целое.

Внутренние силы – силы взаимодействия между материальными точками, входящими в механическую систему: \({F_{{внутр\rm{}}}} = \sum\limits_{i = 1\atopi \ne k}^n {\sum\limits_{k = 1}^n {{F_{ik}}} = 0.}\)

Внешние силы – силы, которые действуют на систему со стороны тел, не входящих в систему.

Замкнутая (изолированная) система – система, на которую не действуют внешние силы.

Рассмотрим систему, состоящую из n материальных точек (или тел) (рис. 6.1).

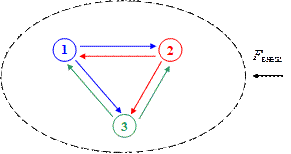
Рис. 6.1

На каждое из трех тел действуют два других тела с силами:

1: \({\vec F_{12}} + {\vec F_{13}}\);

2: \({\vec F_{21}} + {\vec F_{23}}\);

3: \({\vec F_{31}} + {\vec F_{32}}\);

\(\begin{array}{l}{{\vec F}_{12}} + {{\vec F}_{13}} + {{\vec F}_{21}} + {{\vec F}_{23}} + {{\vec F}_{31}} + {{\vec F}_{32}} = 0;\\{{\vec F}_{12}} + {{\vec F}_{21}} = 0.\end{array}\)

Пусть на каждое тело массой m_i действуют внутренние силы \({\vec F_{ik}}\) и внешние силы \(\vec F_i^{в\rm{}}\); тело приобретает скорость 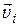. Запишем второй закон Ньютона для каждого тела:

\(\begin{array}{l}\frac{{\rm{d}}}{{dt}}\left( {{m_1}{{\vec v}_1}} \right) = {{\vec F}_{12}} + {{\vec F}_{13}} + ...... + F_1^{в\rm{}};\\\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{m_2}{{\vec v}_2}} \right) = {{\vec F}_{21}} + {{\vec F}_{23}} + ...... + F_2^{в\rm{}};\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{m_n}{{\vec v}_n}} \right) = {{\vec F}_{n1}} + {{\vec F}_{n2}} + ...... + F_n^{в\rm{}}.\end{array}\) (6.1)

Складываем эти уравнения. Так как по третьему закону Ньютона \({\vec F_{ik}} = - {\vec F_{ki}}\), то сумма всех внутренних сил равна нулю.

Имеем

\(\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\sum\limits_{i = 1}^n {{m_i}{{\vec v}_i}} } \right) = \sum\limits_{i = 1}^n {\vec F_i^{в\rm{}}} \). (6.2)

Здесь \(\sum\limits_{i = 1}^n {{m_i}{{\vec v}_i}} \)=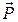 – импульс системы тел, \(\sum\limits_{i = 1}^n {\vec F_i^{в\rm{}}} = {\vec F^{в\rm{}}}\) – равнодействующая всех внешних сил.