Дробно-рациональным уравнением называется уравнение вида \(\frac{P_n(x)}{Q_m(x)}=0\), где \(P_n(x)\) и \(Q_m(x)\)– многочлены.
 Решение дробно-рационального уравнения следует начинать с нахождения области допустимых значений (ОДЗ) переменной, исключив те значения переменной, которые обращают знаменатель \(Q_m(x)\) дроби в нуль.
Таким образом, решение уравнения:

\(\frac{P_n(x)}{Q_m(x)}=0\)

равносильно решению системы: \(\left\{ \begin{array}{l}{P_n}(x) = 0;\\{Q_m}(x) \ne 0.\end{array} \right.\)

Далее решается целое алгебраическое уравнение \(P_n(x)=0\) методами, которые были рассмотрены ранее.

Пример 1. Решить уравнение:

\(\frac{x+1}{2x-2}=\frac{9}{2(x+4)}+\frac{1}{x-1}.\)

Решение. Находим область допустимых значений переменной x:

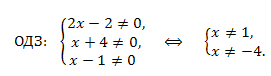
Приводим уравнение к виду:

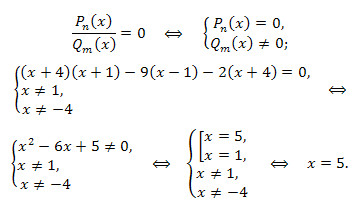
Ответ: x = 5.

Как и при решении любых других уравнений, в некоторых случаях целесообразно применять метод замены переменных.