В алгебре изучаются общие свойства числовых систем с использованием буквенных выражений и общие методы решения задач с помощью уравнений. Числовые системы делятся на числовые и математические выражения.
 Числовое выражение состоит из чисел с указанием операций, которые следует выполнить над ними, и порядка операций.
 Математическое выражение состоит из чисел, обозначенных бук-вами, и цифр с указанием операций, которые следует выполнить над ними, и порядка операций.
Например,

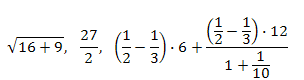
- это числовые выражения;

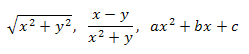
- а это математические выражения.

Обозначим математическое выражение символом \(F(x,y,z,...,t)\) и будем считать, что все входящие в математическое выражение числа и значения переменных \(x,y,z,...,t\) являются действительными числами.

Система чисел \(x_0,y_0,z_0,...,t_0\) называется допустимой системой значений переменных (аргументов), если при \(x=x_0,y=y_0,z=z_0,...,t=t_0\) выражение \(F(x,y,z,...,t)\) можно вычислить.

По другому в этом случае говорят, что выражение \(F(x,y,z,...,t)\)имеет смысл.

Например, область определения выражения \(\sqrt{1-x^2}\) находится из условия \(1-x^2 \geq 0\) и представляет сегмент [–1; 1].

Пусть математические выражения \(F_1(x,y,z,...,t)\) и \(F_2(x,y,z,...,t)\) определены на множестве M₁ и M₂ соответственно, а множество M есть общая часть этих множеств.

Уравнением называется равенство двух математических выражений \(F_1(x,y,z,...,t)\)=\(F_2(x,y,z,...,t)\), в котором системы значений аргументов \(x,y,z,...,t \in M\).

При этом переменные \(x,y,z,...,t\) называются неизвестными, а множество M – областью допустимых значений (ОДЗ) неизвестных \(x,y,z,...,t\).

Система значений неизвестных \(x=x_0,y=y_0,z=z_0,...,t=t_0\) называется решением уравнения, если при подстановке её в уравнение она обращает его в верное равенство.
 В зависимости от того, для какого количества допустимых значе-ний переменных уравнение обращается в верное равенство, оно может иметь конечное число решений, бесконечное множество решений или не иметь решений вообще.

Например, уравнение \(x^2+(y-1)^2=0\) имеет единственное решение x = 0, y = 1.
 Уравнение x = |x| имеет бесконечное множество решений, описываемое неравенством x ≥ 0.
 Уравнение \(|x|+|y|=-1\) не имеет решений вообще.
 Кроме уравнений в алгебре рассматривается ещё одно равенство математических выражений – тождество.
 Тождеством называется равенство двух математических выражений, которое выполняется при всех допустимых значениях входящих в него переменных.
Примерами тождеств являются следующие равенства:

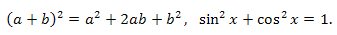
В элементарной математике изучаются только частные виды уравнений, в которых математические выражения \(F_1\) и \(F_2\) являются элементарными функциями.
Уравнения различаются по числу входящих в них неизвестных.
Например,

\(x^2-5x+6=0\) - уравнение с одной неизвестной,

\(|x|+|y|=1\) - уравнение с двумя неизвестными.

Кроме того, уравнения различаются по виду операций, совершаемых над неизвестными. Соответствующая виду операций классификация приведена на схеме (рисунок 1).

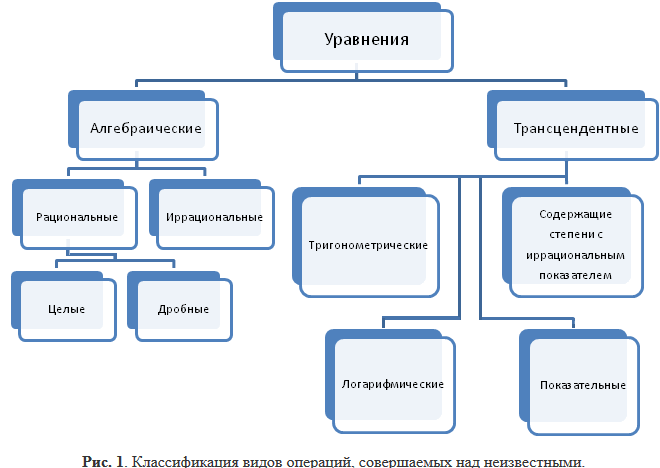
Уравнения называются алгебраическими, если над неизвестными выполняется конечное число операций только следующего вида:

1. сложение,
2. вычитание,
3. умножение,
4. деление,
5. возведение в целую степень,
6. извлечение корня.

Например, каждое из следующих уравнений является алгебраическим:

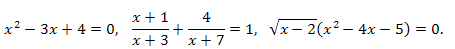
Определения:

Алгебраическое уравнение называется рациональным, если в нём отсутствует извлечение корня из выражения, содержащего неизвестные. Первые два из записанных выше уравнений – рациональные, а третье уравнение – иррациональное.

Рациональное уравнение называется целым, если в нем отсутствует деление на выражение, содержащее неизвестные величины, например, \(x^2-3x+4=0.\)