Пример. Решить уравнение:

\(\frac{x^2-2x}{4x-3}+5=\frac{16x-12}{2x-x^2}.\)

Решение. Находим область допустимых значений переменной x:

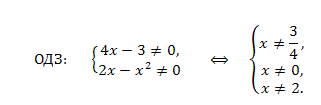
Делаем замену: \(\frac{x^2-2x}{4x-3}=t;t\neq0;\)

получаем и решаем уравнение:

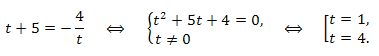
Переходим к переменной x и решаем два уравнения:

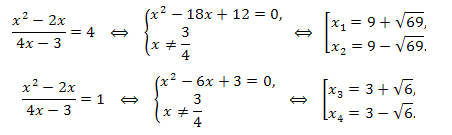
Ответ: \(x=9\pm \sqrt{69};x=3\pm \sqrt{6}.\)

Пример. Решить уравнение:

\(x^2+\frac{1}{x^2}+3(x+\frac{1}{x})-2=0.\)

Решение. Область допустимых значений переменной x есть множество R\{0}.
Сделаем замену \(x+\frac{1}{x}=t\). Возведём обе части этого равенства в квадрат и получим \(x^2+2+\frac{1}{x^2}=t^2,\) откуда находим:

\(x^2+\frac{1}{x^2}=t^2-2.\)

Используя замену переменной, получаем уравнение:

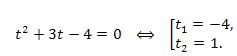
Возвращаемся к переменной x и решаем два уравнения:

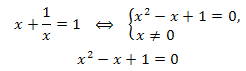
Уравнение \(x^2-x+1=0\) не имеет действительных корней, так как его дискриминант D<0, а:

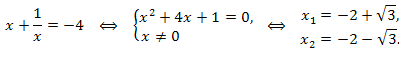
Ответ: \(x=-2\pm \sqrt{3}.\)

Пример. Решить уравнение:

\((x-3)(x+6)(x^2-2x-8)=126x^2.\)

Решение. Область допустимых значений переменной x есть множество R.
Преобразуем уравнение таким образом, чтобы можно было сделать замену переменной. Для этого разложим трёхчлен \(x^2-2x-8\) на множители:

\(x^2-2x-8=(x-4)(x+2).\)

Тогда исходное уравнение примет вид:

\((x-3)(x+6)(x-4)(x+2)=126x^2.\)

Поскольку x = 0 не является корнем уравнения, обе части уравнения можно почленно разделить на \(x^2\). После этого уравнение приобретает вид:

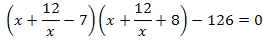
Далее делаем замену переменной \(x+\frac{12}{x}=t;t\in R;\) и решаем полученное уравнение:

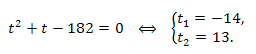
Возвращаясь к переменной x, получаем и решаем два уравнения:

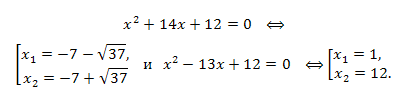
Ответ: \(x_1=-7\pm \sqrt{37};x_2=1;x_3=12.\)