Алгебраическим уравнением степени n называется уравнение вида:

\(a_nx^n+a_{n-1}x^{n-1}+...+a_0=0,\)

где \(a_0,a_1,..,a_n\) – коэффициенты уравнения, причём \(a_n\neq0.\)
 Основными методами решения алгебраических уравнений степени n являются метод разложения многочлена на множители и метод замены переменной. Следующие теоремы позволяют в некоторых случаях провести подбор корня уравнения и, применяя метод разложения на множители, понизить порядок уравнения, сводя его к квадратным и линейным уравнениям.

Теорема 1. Если \(x_0\) – корень уравнения \(f(x)=0\), где:

\(f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_0,\)

то \(f(x)\) делится без остатка на \(x-x_0.\)

Теорема 2. Если все коэффициенты алгебраического уравнения являются целыми числами, то всякий целый корень уравнения является делителем свободного члена \(a_0\) уравнения.
 Таким образом, если известен один корень \(x=x_0\) алгебраического уравнения \(f(x)=0\), то:

\(f(x)=(x-x_0)g(x),\)

где \(g(x)\) - многочлен, степень которого равна n – 1, и нахождение остальных корней уравнения \(f(x)=0\) сводится к решению уравнения \(g(x)=0.\)

Пример. Решить уравнение:

\(x^4-4x^3-13x^2+28x+12=0.\)

Решение.
а) запишем делители числа 12: \(\pm 1; \pm 2;\pm3;\pm4;\pm6;\pm12.\)
б) последовательно подставляя эти числа в уравнение, находим один из корней уравнения x = 2.
в) произведём деление многочлена «уголком» на разность x –2:

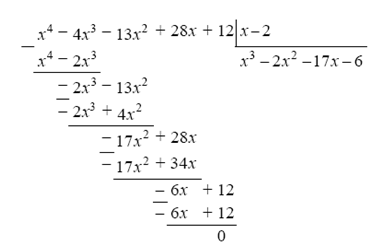
Получаем уравнение:

\((x-2)(x^3-2x^2-17x-6)=0.\)

Выписывая делители числа –6 и убедившись в том, что x – 3 является корнем многочлена \(x^3-2x^2-17x-6,\) получаем равенство:

\((x-2)(x+3)(x^2-5x-2)=0.\)

Решив и квадратное уравнение, укажем все четыре корня исходного уравнения:

\(\left[ \begin{array}{l}{x_1} = 2;\\{x_2} = - 3;\\{x_3} = \frac{{5 + \sqrt {33} }}{2};\\{x_4} = \frac{{5 - \sqrt {33} }}{2}.\end{array} \right.\)

Количество корней решённого уравнения иллюстрирует основную теорему алгебры.
Теорема. Каждое алгебраическое уравнение степени n имеет ровно n корней. Среди этих корней могут быть не только действительные, но и комплексные числа.
 При решении алгебраических уравнений степени n… 2 можно применять следующие приёмы:

1. Вынесение общего множителя за скобки.
2. Группировку членов многочлена с последующим вынесением общего множителя за скобки.
3. Использование формул сокращённого умножения.