При решении иррациональных неравенств с целью рационализации применяется, как правило, возведение в соответствующую степень обеих частей неравенства.
 При этом следует помнить, что при возведении обеих частей неравенства в нечётную степень всегда получается неравенство, равносильное исходному неравенству.
 Если же обе части неравенства возводятся в чётную степень, то неравенство, равносильное исходному неравенству, получается лишь в том случае, когда обе части неравенства неотрицательны. Приведём схемы решения некоторых иррациональных неравенств:

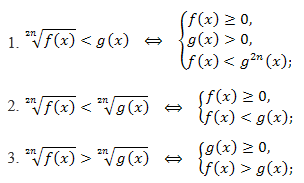
 4. О знаке правой части неравенства \(\sqrt[2n]{f(x)}>g(x)\) ничего определённого сказать нельзя, поэтому следует рассматривать два случая:

а) \(g(x)<0;\)

б) \(g(x)\geq0.\)

Таким образом, неравенство \(\sqrt[2n]{f(x)}>g(x)\) будет равносильно совокупности двух систем неравенств:

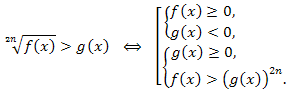
Пример. Решить неравенство:

\(\sqrt{x+1}<\sqrt {x^2+x+3}.\)

Решение. Согласно пункту 3:

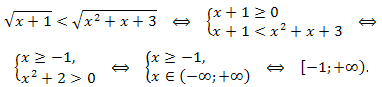
Ответ: \(x\in [-1;+\infty).\)

Пример. Решить неравенство:

\(\sqrt{5x-x^2}<x-2.\)

Решение. Согласно пункту 1:

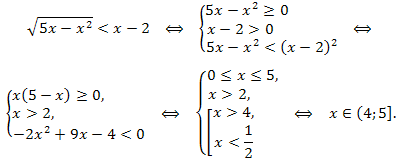
Ответ: \(x\in (4;5].\)