При решении неравенств, содержащих переменную под знаком модуля, область допустимых значений следует разбить на интервалы, в каждом из которых выражения, стоящие под знаком модуля, сохраняют знак. Затем неравенство решается на каждом таком интервале и полученные решения объединяются в множество решений исходного неравенства.
Пример 1. Решить неравенство:

\(x+|x+1|>2.\)

Решение. Точкой x = 1 числовая прямая разбивается на два промежутка \((-\infty;-1)\) и \([-1;+\infty).\) С учетом разбиения заданное неравенство равносильно совокупности двух систем:

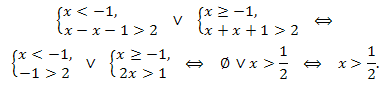
Первая система неравенств не имеет решения, поэтому получаем:

\(x\in(1/2;+\infty).\)

Рассмотрим схемы решения некоторых неравенств с модулем.

1 схема

Решение неравенства \(|f(x)|<g(x)\) на множестве определения функций f(x) и g(x) равносильно системе неравенств:

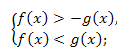
при \(g(x)\leq0\) неравенство не имеет решений. В частности, неравенство \(|f(x)|<a\) при a>0 равносильно системе \(-a<f(x)<a,\) а при a ≤ 0 не имеет решений.

2 схема

Неравенство \(|f(x)|>g(x)\) в области допустимых значений равносильно совокупности неравенств:

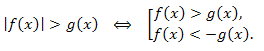
В частности, неравенство \(|f(x)|>a\) при a ≥ 0 равносильно совокупности неравенств:

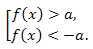
При a < 0 неравенство \(|f(x)|>a\) справедливо при всех значениях x из области определения функции f(x).

3 схема

Неравенство вида:

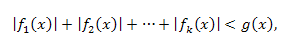
содержащее несколько различных функций под знаком модуля, рационально решать методом интервалов.
На числовой прямой отмечаем значения x, при которых функция, стоящая под знаком модуля, равна нулю. Эти точки разбивают прямую на интервалы, каждый из которых является интервалом знакопостоянства функций \(f_1(x),f_2(x),...,f_k(x).\)
Затем на каждом из интервалов неравенство решается без знака абсолютной величины. Объединяя найденные на всех интервалах решения исходного неравенства, получаем множество всех его решений.

4 схема

Решение неравенства вида \(|f(x)|>|g(x)|\) можно осуществить методом интервалов. Однако неравенство подобного вида рациональнее решать переходом к неравенству вида:

\(f^2(x)>g^2(x).\)

5 схема

Неравенство вида:

\(ax^2+b|x|+c<0\)

или

\(ax^2+b|x|+c>0\)

рекомендуется решать с помощью замены \(|x|=t,t\geq0.\)