Пример. Решить неравенство

\(\sqrt{5x-x^2}<x-2.\)

Решение. Применяем 1 схему решения, получаем:

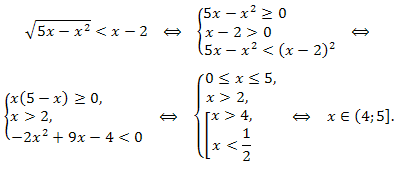
Ответ: \(x\in (4;5].\)

Пример. Решить неравенство

\(\sqrt{x^2+5x-24}>x-1.\)

Решение. Применяем 4 схему решения, получаем:

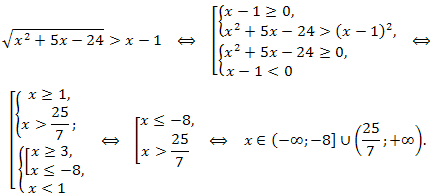
Ответ: \(x\in (-\infty;-8]\cup (25/7;+\infty).\)

Пример. Решить неравенство

\(\sqrt{x^2-x-2}(x-1)\geq0.\)

Решение. Так как \(\sqrt{x^2-x-2}\geq0,\) в области допустимых значений переменной x, то неравенство:

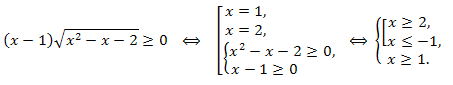
Ответ: \(x\in [2;+\infty)\cup \{-1\}.\)

Пример. Решить неравенство

\(\sqrt{2x-4}-\sqrt{x+5}>1.\)

Решение. Уединяем один радикал так, чтобы обе части неравенства были неотрицательными. Составляем равносильную ему систему:

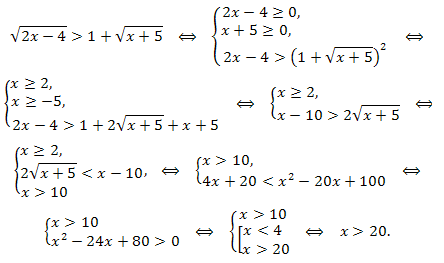
Ответ: \(x\in (20;+\infty).\)

Пример. Решить неравенство

\(\sqrt[3]{x^3+2x^2-5x+3}<x.\)

Решение.

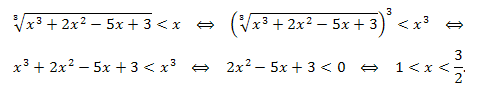
Ответ: \(x\in (1;3/2).\)