Пример . Решить неравенство:

\(|x-1|+|x-2|>3+x.\)

Решение. Находим нули функций:

\(y_1=x-1;y_2=x-2;\)

\(x_1=1;x_2=2.\)

Точки x = 1, x = 2 разбивают числовую прямую на три промежутка:

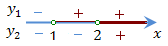
Над каждым из промежутков числовой прямой поставлены знаки функций. Исходное неравенство равносильно совокупности трех систем неравенств:

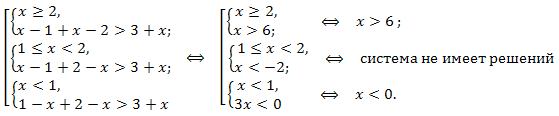
Решением неравенства являются два промежутка:

\(x\in(-\infty;0)\cup (6;+\infty).\)

Пример . Решить неравенство:

\(|x-2|<|x-4|.\)

Решение. В соответствии со схемой решения 4 неравенство:

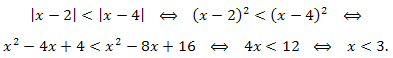
Ответ: \(x\in (-\infty;3).\)

Пример . Решить неравенство:

\(|x^2-3x-5|>|x^2-2x-2|.\)

Решение. В соответствии со схемой решения 4:

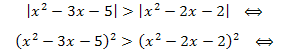
Используем формулу разности квадратов:

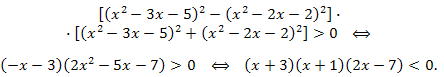
Решаем полученное неравенство методом интервалов и находим:

\(x \in (-\infty;-3)\cup (-1;3.5).\)