Пример. Решить неравенство:

\(|x^2+2x|\leq x.\)

Решение. Так как неравенство:

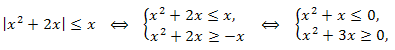
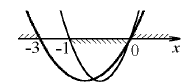
решением первого неравенства системы является множество \(x\in [-1;0],\) а второго неравенства \(x \in (-\infty;-3]\cup [0;+\infty).\) поэтому решением системы является x = 0.

Пример. Решить неравенство:

\(|x-5|<9.\)

Решение.

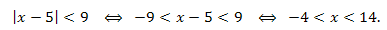
Ответ: \(x \in (-4;14).\)

Пример. Решить неравенство:

\(|x^2-2x|\geq12-x^2.\)

Решение. В соответствии со схемой решения 2 имеем:

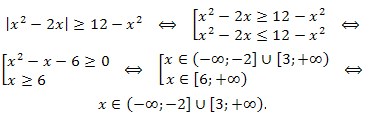
Ответ: \(x \in (-\infty;-2]\cup [3;+\infty).\)

Пример. Решить неравенство:

\(|2+\frac{1}{x}|>3.\)

Решение.

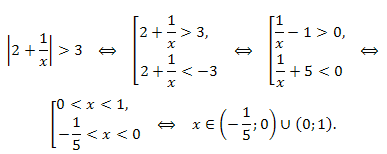
Ответ: \(x \in (-\frac{1}{5};0)\cup (0;1).\)

Пример. Решить неравенство:

\(x^2-6|x|+5<0.\)

Решение. Выполним замену \(|x|=t,t\geq0.\) Получаем и решаем неравенство :

\(t^2-6t+5<0;\)

\(1<t<5.\)

Возвращаемся к переменной x, записываем и решаем систему неравенств:

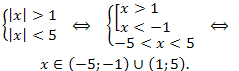
Ответ: \(x \in (-5;-1)\cup (1;5).\)