Пример 2. Потенциальная энергия тела массой m, находящегося в точке N на расстоянии r от тела массой M.

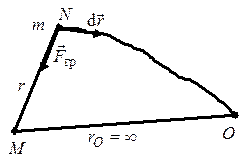
Рис. 4.13

Тело массой M является источником гравитационного поля (рис. 4.13). За начало отсчета потенциальной энергии выберем точку О (на бесконечно большом удалении \({r_O} = \infty \) от тела массой M). Потенциальная энергия материальной точки (тела) в точке N равна работе А_NO гравитационной силы, совершаемой при перемещении тела из точки N в точку O по произвольной траектории. Работа гравитационной силы будет рассчитана по формуле

\(A = \int\limits_N^O {\delta A} = \int\limits_N^O {({{\vec F}_{{\rm{гр}}}}{\rm{d}}\vec r) = - \int\limits_r^{{r_O}} {{\rm{\gamma }}\frac{{Mm}}{{{r^2}}}{\rm{d}}r = {\rm{\gamma }}Mm \cdot \left( {\frac{1}{{{r_O}}} - \frac{1}{r}} \right)} } = - {\rm{\gamma }}\frac{{Mm}}{r}\).

Как следует из полученного выражения, если начало отсчета потенциальной энергии – точка О – выбрано «в бесконечности» (\({r_O} = \infty \)), то потенциальная энергия тела (материальной точки) во всех точках пространства вокруг тела массой М отрицательна.