Итак, работа консервативной силы определяется разностью потенциальной энергии тела в начальной и конечной точках пути. При элементарном перемещении работа равна минус изменению потенциальной энергии:

\({\rm{d}}A = \left( {\vec F{\rm{d}}\vec r} \right) = - {\rm{d}}{E_{\rm{п}}}\). (4.25)

Знак минус говорит о том, что работа совершается за счет убыли потенциальной энергии.

Работа консервативных сил на конечном участке пути 1–2

\({A_{12}} = \int\limits_1^2 {\left( {\vec F{\rm{d}}\vec r} \right) = - \left( {{E_{{\rm{п}}2}} - {E_{{\rm{п}}1}}} \right)} = {E_{{\rm{п1}}}} - {E_{{\rm{п2}}}}\). (4.26)

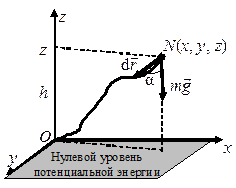
Рис. 4.12

Потенциальная энергия – функция, которая определяется с точностью некоторой произвольной постоянной, определяющей нулевой уровень потенциальной энергии. Так как в формулу работы консервативной силы входит только разность значений \({E_{\rm{п}}}\) в двух положениях частицы, то нулевой уровень отсчета энергии выбирают произвольно. То есть потенциальную энергию тела в каком-то определенном положении считают равной нулю. Энергию тела в других положениях отсчитывают относительно нулевого уровня. Тело, находящееся в поле консервативных сил, обладает потенциальной энергией E_п относительно нулевого уровня потенциальной энергии.

Конкретный вид функции E_п зависит от характера силового поля.

Для определения потенциальной энергии тела (материальной точки) в консервативном силовом поле необходимо выбрать положение начала отсчета нулевого уровня потенциальной энергии и вычислить работу силы при перемещении по произвольной траектории в этом поле из данной точки поля в точку отсчета нулевого уровня потенциальной энергии.