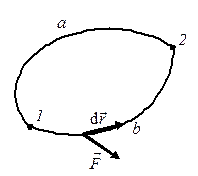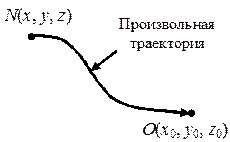Пусть имеется консервативное силовое поле. Материальная точка (тело) расположена в точке N(x, y, z) этого поля (рис. 4.10). Выберем произвольную точку О этого поля (ее координаты x₀, y₀, z₀) и назовем ее началом отсчета потенциальной энергии. В точке О потенциальная энергия материальной точки равна нулю.

Потенциальной энергией материальной точки в точке Nконсервативного поля называется работа сил поля, совершаемая при перемещении материальной точки из точки N в точку О, принятую за начало отсчета потенциальной энергии:\({E_{\rm{п}}} = \int\limits_N^O {(\vec F{\rm{d}}\vec r)} \), где \(\vec F\) – сила поля; интеграл вычисляется по произвольной траектории между точками N и О.

Так как поле консервативное, то потенциальная энергия является только функцией координат x, y, z точки поля, в которой расположена материальная точка.

Так как поле консервативное, то потенциальная энергия является только функцией координат x, y, z точки поля, в которой расположена материальная точка.

Рис. 4.11

Если материальная точка под действием консервативных сил поля перемещается из произвольного начального положения 1 в произвольное конечное положение 2 (рис. 4.11), то работа этих сил равна убыли потенциальной энергии материальной точки: \({A_{1 - 2}} = {E_{{\rm{п}}1}} - {E_{{\rm{п}}2}}\), где \( {E_{{\rm{п}}1}}\) и \( {E_{{\rm{п}}2}}\) – потенциальная энергия материальной точки в начальном и конечном положениях. Так как работа консервативных сил не зависит от формы траектории, то найдем работу консервативных сил по двум траекториям, одна из которых проходит через точку О – начало отсчета потенциальной энергии. Обозначим \({A_{1 - 2}}\) – работу по траектории 1–2, \({A_{1 - O - 2}}\) – работу по траектории 1–О–2. Так как поле консервативное, то \({A_{1 - 2}} = {A_{1 - O - 2}}\).

Представим \({A_{1 - O - 2}}\) как сумму работ на участках 1–О и О–2 по траектории 1–О–2, получим \({A_{1 - 2}} = {A_{1 - O - 2}} = {A_{1 - O}} + {A_{O - 2}} = {A_{1 - O}} - {A_{2 - O}}\).

Из определения потенциальной энергии \({A_{1 - O}} = {E_{{\rm{п}}1}},\quad {A_{2 - O}} = {E_{{\rm{п}}2}}\), тогда

\({A_{1 - 2}} = {E_{{\rm{п}}1}} - {E_{{{п}}2}} = - ({E_{{\rm{п}}2}} - {E_{{\rm{п}}1}}) = - \Delta {E_{\rm{п}}}\). (4.23)

Элементарная работа консервативных сил

\(\delta A = - {\rm{d}}{E_{\rm{п}}}\). (4.24)

Выражения (4.23) и (4.24) определяют связь работы консервативных сил с изменением потенциальной энергии поля (в интегральной и дифференциальной формах соответственно).