Если материальная точка находится в консервативном силовом поле и известна зависимость действующей на материальную точку силы от координаты N (x, y, z) точки поля, то легко можно найти потенциальную энергию поля в этой точке

\({E_{\rm{п}}}(x,y,z) = \int\limits_N^O {(\vec F{\rm{d}}\vec r)} \), (4.27)

где интеграл вычисляется вдоль произвольной траектории между точкой N и точкой О, принятой за начало отсчета потенциальной энергии.

Потенциальная энергия тела является функцией от его координат:

E_п = E_п (x, y, z). (4.28)

Зная вид этой функции, можно найти силу, действующую на тело. Установим связь между потенциальной энергией и силой.

Рассмотрим перемещение тела под действием силы 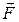. Разложим силу на три составляющие вдоль координатных осей и рассмотрим работу каждой составляющей силы:

\(\vec F = \vec i{F_x} + \vec j{F_y} + \vec k{F_z}\), \({\rm{d}}\vec r = \vec i{\rm{d}}x + \vec j{\rm{d}}y + \vec k{\rm{d}}z\). (4.29)

Тогда \({\rm{d}}A = (\vec F{\rm{d}}\vec r) = {F_x}{\rm{d}}x + {F_y}{\rm{d}}y + {F_z}{\rm{d}}z = - {\rm{d}}{E_{\rm{п}}}(x,y,z)\).

Чтобы определить компоненты вектора силы, поступим следующим образом. Пусть, совершая элементарное перемещение, материальная точка движется параллельно оси x (вектор \({\rm{d}}\vec r\) параллелен оси x). В этом случае координаты y и z материальной точки остаются постоянными (y= const, z= const), значит dy = dz= 0. Тогда

\({F_x}{\rm{d}}x = - {\left[ {{\rm{d}}{E_{\rm{п}}}(x,y,z)} \right]_{y,z = {\rm{const}}}}\). (4.30)

Отсюда

\({F_x} = - {\left[ {\frac{{{\rm{d}}{E_{\rm{п}}}(x,y,z)}}{{{\rm{d}}x}}} \right]_{y,z = {\rm{const}}}} = - \frac{{\partial {E_{\rm{п}}}(x,y,z)}}{{\partial x}}\). (4.31)

Здесь\(\frac{{\partial {E_{\rm{п}}}}}{{\partial x}}\) – частная производная функции E_п(x, y, z), вычисленная в предположении, что переменные y и z остаются неизменными, а изменяется лишь величина x.

Итак,

\({F_x} = - \frac{{\partial {E_{\rm{п}}}}}{{\partial x}}\), \({F_y} = - \frac{{\partial {E_{\rm{п}}}}}{{\partial y}}\), \({F_z} = - \frac{{\partial {E_{\rm{п}}}}}{{\partial z}}\). (4.32)

Эти три формулы можно объединить в одну векторную формулу. С этой целью умножим их на единичные векторы координатных осей \(\vec i,\vec j,\vec k\) и сложим:

\(\vec F = {F_x}\vec i + {F_y}\vec j + {F_z}\vec k\),

или

\(\vec F = - \left( {\frac{{\partial {E_{\rm{п}}}}}{{\partial x}}\vec i + \frac{{\partial {E_{\rm{п}}}}}{{\partial y}}\vec j + \frac{{\partial {E_{\rm{п}}}}}{{\partial z}}\vec k} \right).\) (4.33)

Выражение, стоящее в скобках, называют градиентом функции\({E_{\rm{п}}}\) и обозначают \(\overrightarrow {{\rm{grad}}} {E_{\rm{п}}}\): \(\vec F = - \overrightarrow {{\rm{grad}}} \,{E_{\rm{п}}} = - \nabla {E_{\rm{п}}}\).

Градиентом скалярной функции E_п(x, y, z) называется векторная функция, которая по определению равна

\(\overrightarrow {{\rm{grad}}} \,{E_{\rm{п}}} = \frac{{\partial {E_{\rm{п}}}}}{{\partial x}}\vec i + \frac{{\partial {E_{\rm{п}}}}}{{\partial y}}\vec j + \frac{{\partial {E_{\rm{п}}}}}{{\partial z}}\vec k\). (4.34)

Градиент представляет собой оператор, т.е. правило, по которому всякой скалярной функции E_п (x, y, z) ставится в соответствие векторная функция тех же переменных. Градиент скалярной функции указывает направление наиболее быстрого возрастания функции.

Сила равна градиенту потенциальной энергии, взятому с обратным знаком. Знак минус означает, что сила всегда направлена в сторону уменьшения потенциальной энергии.

Эквипотенциальной поверхностью называется поверхность, во всех точках которой потенциальная энергия имеет одно и то же значение (поверхность постоянной потенциальной энергии). Уравнение эквипотенциальной поверхности можно записать как \({E_{\rm{п}}}(x,y,z) = {\rm{const}}\).