Любая обыкновенная дробь допускает представление в виде бесконечной десятичной дроби. Так дробь \(\frac{1}{4}\) может быть записана не только в виде конечной десятичной дроби:

\(\frac{1}{4}=\frac{1\cdot 25}{4\cdot 25}=\frac{25}{100}=0,25;\)

но и в виде бесконечной десятичной дроби, если вместо отсутствующих десятичных знаков записать нули, т.е.

\(\frac{1}{4}=0,25=0,25000...\)

Возьмем другую дробь \(\frac{5}{14}\) которая не допускает представления в виде конечной десятичной дроби и будем выполнять деление, анализируя частное:

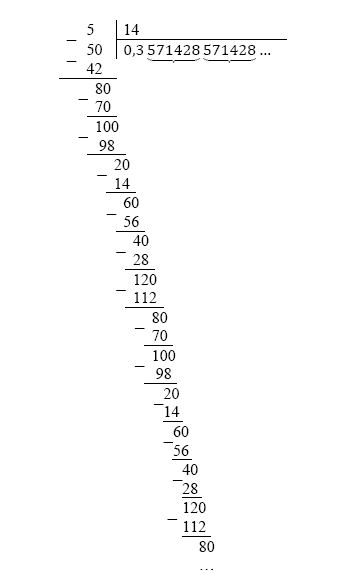
Отмечаем, что в частном возникают периодически повторяющиеся группы цифр.
Бесконечная десятичная дробь, в записи которой несколько цифр повторяются в неизменном порядке, называется периодической.
Совокупность повторяющихся цифр называется периодом.
Для краткости период записывают один раз, заключая его в круглые скобки. Например,

\(\frac{5}{14}=0,3(571428).\)

Десятичная дробь называется чисто периодической, если период начинается сразу после запятой. Например,

\(\frac{1}{3}=0,333...=0,(3).\)

Если же между запятой и периодом есть десятичные знаки, то дробь называется смешанной периодической.
Например, 0,3(571428).
 Таким образом, оказывается верным утверждение: любая обыкновенная дробь представима в виде бесконечной десятичной дроби.
 Часто встречается и обратная операция – обращение периодической дроби в обыкновенную. Идею решения такой задачи рассмотрим на примерах.