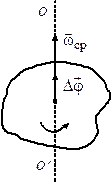Пусть за время \(\Delta t\) тело повернулось на угол \(\Delta \phi \).

Средняя угловая скорость – это физическая величина, равная отношению вектора углового перемещения к промежутку времени, за который это перемещение произошло:

\({\vec \omega _{ср{\rm{}}}} = \frac{{\Delta \vec \phi }}{{\Delta t}}\). (2.2)

Средняя угловая скорость – это вектор, направление которого совпадает с вектором \(\Delta \phi \). Значит, вектор средней угловой скорости направлен по оси вращения и определяется правилом правого винта.

Мгновенная угловая скорость – это угловая скорость в данный момент времени. Мгновенная угловая скорость равна отношению элементарного углового перемещения (углового перемещения за бесконечно малое время) к промежутку времени, за который это перемещение произошло. Если время движения бесконечно мало \(\Delta t \to 0\), то угловое перемещение \(\Delta \vec \phi \to {\rm{d}}\vec \phi \), значит, мгновенная угловая скорость – это предел, к которому стремится средняя угловая скорость при \(\Delta t \to 0\):

\(\vec \omega = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \vec \phi }}{{\Delta t}} = \frac{{{\rm{d}}\vec \phi }}{{dt}}\), \(\begin{array}{*{20}{c}}{}&{\begin{array}{*{20}{c}}{}&{\vec \omega \uparrow \uparrow {\rm{d}}\vec \varphi ,\begin{array}{*{20}{c}}{}&{\left[ \omega \right] = \frac{{{рад\rm{}}}}{{с\rm{}}}}\end{array}.}\end{array}}\end{array}\) (2.3)

Векторная величина, равная первой производной от угла поворота тела по времени, называется мгновенной угловой скоростью.

Угловое перемещение \({\rm{d}}\vec \phi \) – векторная величина (псевдовектор, аксиальный вектор), а модуль \(\left| {{\rm{d}}\vec \phi } \right|\) равен углу поворота за время dt.

Направление 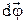 определяется правилом правого винта:

\(\vec \omega = \frac{{{\rm{d}}\vec \phi }}{{{\rm{d}}t}}\); \(\begin{array}{*{20}{c}}{}&{\begin{array}{*{20}{c}}{}&{\vec \omega \uparrow \uparrow {\rm{d}}\vec \phi }\end{array}}\end{array}\);

направление \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \omega } \) также определяется правилом правого винта.

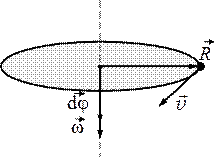
Угловая скорость \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \omega } \) направлена вдоль оси, вокруг которой вращается тело, в сторону, определяемую правилом правого винта (рис. 2.6).