Вращательное движение абсолютно твердого тела относительно неподвижной оси – движение, при котором все точки тела движутся по окружностям, центры которых лежат на прямой линии, называемой осью вращения.

При вращательном движении точки тела, находящиеся на разном расстоянии от оси вращения, за одинаковые промежутки времени имеют разные перемещения и разные скорости и ускорения.

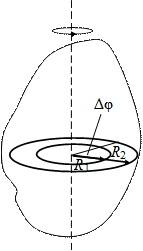
В то же время радиус-вектор, соединяющий точки тела с осью вращения, за одинаковые промежутки времени поворачивается на один и тот же угол Δφ (рис. 2.3).

Введем понятие вектора углового перемещения. Вектор углового перемещения \(\Delta \vec \phi \) – это вектор, определяющий, как вращается твердое тело. Направление вектора \(\Delta \vec \phi \) определяется правилом правого винта: если головку винта вращать в направлении вращении тела, то направление поступательного движения винта совпадает с направлением вектора \(\Delta \vec \phi \).

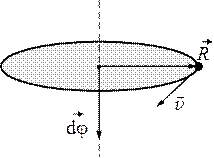
Если время вращения бесконечно мало, угловое перемещение будет \({\rm{d}}\vec \phi \) (рис. 2.4). Угловое перемещение\({\rm{d}}\vec \phi \)– векторная величина (псевдовектор, аксиальный вектор), а модуль \(|{\rm{d}}\vec \phi| \) равен углу поворота. Направление \({\rm{d}}\vec \phi \) определяется правилом правого винта.