Пусть твердое тело вращается вокруг неподвижной оси ОО' (рис. 5.4). Мысленно разобьем тело на материальные точки массой m_i. Каждая материальная точка движется по окружности радиуса r_i с линейной скоростью \({\vec v_i}\). Кинетическая энергия вращающегося тела равна сумме кинетических энергий этих точек:

\({E_{к\rm{}}} = \sum\limits_i {\frac{{{m_i}v_i^2}}{2}} \). (5.10)

Линейная скорость материальной точки зависит от расстояния до оси вращения r_i:

\({v_i} = \omega {r_i}\), (5.11)

где 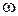 – угловая скорость тела.

Отсюда \({E_{к\rm{}}} = \frac{{{\omega ^2}}}{2}\sum\limits_i {{m_i}r_i^2} \), т.к. \(I = \sum\limits_{i = 1}^n {{m_i}} r_i^2\), то

\({E_{к\rm{}}} = \frac{{I{\omega ^2}}}{2}\), (5.12)

где I – момент инерции тела относительно оси вращения; 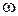 – его угловая скорость.

В случае плоского движения тела, например шара, скатывающегося с наклонной плоскости без скольжения, энергия складывается из энергии поступательного движения и энергии вращения:

\({E_{к\rm{}}} = \frac{{mv_c^2}}{2} + \frac{{{I_c}{\omega ^2}}}{2}\), (5.13)

где m – масса тела; \({v_c}\) – скорость центра масс тела; I_c – момент инерции тела относительно оси, проходящей через его центр масс; \(\omega \) – угловая скорость тела.