Абсолютно твердое тело – вторая абстракция, с которой имеют дело в механике. В природе нет совершенно недеформируемых тел. Однако во многих случаях деформациями можно пренебречь.

Абсолютно твердым телом называется тело, деформациями которого можно пренебречь в условиях данной задачи.

Простейшими типами движения абсолютно твердого тела являются поступательное движение и вращательное движение вокруг неподвижной оси (рис. 2.1). Любое сложное движение твердого тела можно представить как совокупность поступательного и вращательного движений.

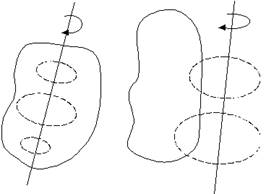
Поступательное движение Вращательное движение

Рис. 2.1

Поступательное движение – это такое движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе. При поступательном движении все точки тела движутся одинаково, имеют одинаковые скорости и ускорения. Поэтому изучение движения твердого тела можно свести к изучению движения отдельных точек тела, т.е. к задаче кинематики точки.

Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях, причем центры окружностей лежат на оси вращения.

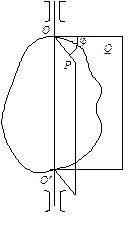
Рис. 2.2

Будем рассматривать вращение тела вокруг неподвижной оси ОО' (рис. 2.2). Проведем через ось ОО' две плоскости: \(Q\) – неподвижная плоскость, она будет служить системой отсчета;
P – подвижная плоскость, которая вращается вместе с телом.

Угол j однозначно определяет мгновенное положение подвижной плоскости, а значит и тела. Итак, угол 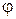 есть функция времени:

\(\phi \) = \(\phi \)(t). (2.1)

Уравнение (2.1) называется кинематическим уравнением вращательного движения. Вид функции зависит от характера движения.