Физика
1.1.9. Твердое тело. Поступательное и вращательное движение твердого тела
Момент импульса
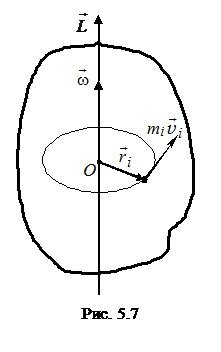
Рассмотрим движение отдельных точек тела, вращающегося вокруг неподвижной оси (рис. 5.7). Каждая из них массой mi движется по окружности постоянного радиуса ri. Ее линейная скорость \({\vec v_i}\), импульс \({m_i}{\rm{ }}{\vec v_i}\). Скорость и импульс перпендикулярны радиусу, т.е. радиус является плечом вектора \({m_i}{\rm{ }}{\vec v_i}\). Поэтому можно записать, что момент импульса данной точки равен
\({L_i} = {m_i}{\rm{ }}{v_i}{\rm{ }}{r_i}\), \({\vec L_i} = \left[ {{{\vec r}_i}{{\vec P}_i}} \right]\) (5.22)
и направлен по оси вращения в сторону, определяемую правилом правого винта. Учитывая, что \({v_i} = \omega {r_i}\), получим
 \({L_i} = {m_i}r_i^2\omega = {I_i}{\omega _i}\), (5.23)
\({L_i} = {m_i}r_i^2\omega = {I_i}{\omega _i}\), (5.23)
где \({I_i}\) – момент инерции материальной точки 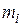 относительно оси вращения.
относительно оси вращения.
Момент импульса твердого тела относительно оси равен сумме моментов импульсов всех его точек:
\(L = \sum\limits_i {} {I_i}\omega \),
или
\(L = \sum\limits_i {{m_i}r_i^2\omega = \omega \sum\limits_i {{m_i}} } r_i^2 = I\omega \). (5.24)
Итак, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно этой же оси на угловую скорость.
Учитывая, что векторы \(\vec L\) и \(\vec \omega \) имеют одинаковое направление, придем к соотношению
\(\vec L = I\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \omega } \). (5.25)
При описании динамики вращательного движения момент импульса играет такую же роль, что и импульс при поступательном движении.
Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (табл. 5.2).
Таблица 5.2
| Поступательное движение | Вращательное движение | ||
| Масса | \({m}\) | Момент инерции | \({I}\) |
| Скорость | \(\vec v = \frac{{{\rm{d}}\vec r}}{{{\rm{d}}t}}\) | Угловая скорость | \(\vec \omega = \frac{{{\rm{d}}\vec \phi }}{{{\rm{d}}t}}\) |
| Ускорение | \(\vec a = \frac{{{\rm{d}}\vec v}}{{{\rm{d}}t}}\) | Угловое ускорение | \(\vec \varepsilon = \frac{{{\rm{d}}\vec \omega }}{{{\rm{d}}t}}\) |
| Сила | \(\vec F\) | Момент силы | \(\vec M\) |
| Импульс | \(\vec P = m\vec v\) | Момент импульса | \(\vec L = I\vec \omega \) |
| Основное уравнение | \(\vec F = m\vec a\) | Основное уравнение динамики | \(\vec M = I\vec \varepsilon \) |
| Работа | \({\rm{d}}A = {F_S}{\rm{d}}S\) | Работа | \({\rm{d}}A = M{\rm{d}}\phi \) |
| Кинетическая энергия | \(\frac{{m{v^2}}}{2}\) | Кинетическая энергия | \(\frac{{I{\omega ^2}}}{2}\) |
Другие материалы по данной теме
Определение
Поступательное движение
Видео
Поступательное движение твердого тела
Формула
\({a_\tau } = \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = R\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = R\varepsilon \)
