Если известен момент инерции тела относительно оси, проходящей через его центр масс, то можно найти момент инерции относительно любой другой параллельной оси. Для этого надо воспользоваться теоремой Гюйгенса – Штейнера:

момент инерции тела I относительно произвольной оси равен моменту его инерции I_c относительно параллельной ей оси, проходящей через центр масс C тела, сложенному с произведением массы тела m на квадрат расстояния a между осями:

\(I = {I_c} + m{a^2}\). (5.6)

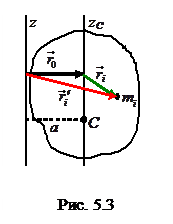
Найдем связь между моментами инерции тела относительно двух параллельных осей, одна из которых проходит через центр масс. Найдем момент инерции тела относительно оси z, параллельной оси z_C. Ось z_C проходит через центр масс тела. Разделим мысленно тело на частицы массой m_i, где i – порядковый номер. Определим положение каждой частицы относительно осей z и z_C. В соответствии с определением момента инерции \({I_i} = {m_i}r_i^2\), где \({r_i}\) – это кратчайшее расстояние до оси вращения (радиус окружности, которую описывает точка при своем движении вокруг оси вращения).

На рис. 5.3 видно, что \({\vec r'_i} = {\vec r_i} + {\vec r_0}\), тогда момент инерции точки массой m_i относительно оси z равен , а для всего тела момент инерции относительно оси z равен сумме моментов инерции всех частиц тела относительно этой же оси:

\(\begin{array}{l}{I_z} = \sum\limits_i {{I_i}} = \sum\limits_i {{m_i}{{r'}_i}^2} = \sum\limits_i {{m_i}{{({{\vec r}_i} + {{\vec r}_0})}^2}} = \\ = \sum\limits_i {{m_i}{r_i}^2 + \sum\limits_i {{m_i}r_0^2 + 2\sum\limits_i {{m_i}({{\vec r}_i} \cdot {{\vec r}_0})} } } .\end{array}\) (5.7)

По определению \({I_{{z_C}}} = \sum\limits_{} {{m_i}r_i^2} \) – момент инерции тела относительно оси z_C, проходящей через центр масс тела; \(\sum\limits_i {{m_i} = m} \), тогда \(\sum\limits_i {{m_i}r_0^2 = m{a^2}} \). Выражение \(2\sum\limits_i {{m_i}({{\vec r}_i} \cdot {{\vec r}_0})} \) можно преобразовать: \(2\sum\limits_i {{m_i}({{\vec r}_i} \cdot {{\vec r}_0})} = 2(\sum\limits_i {{m_i}{{\vec r}_i} \cdot {{\vec r}_0})} \). Величина, равная \(\sum\limits_i {{m_i}{{\vec r}_i}} = m{\vec r_C}\), определяет положение центра масс тела относительно оси z_C. Из рисунка видно, что \({\vec r_C} = 0\), т.к. центр масс лежит на оси z_C.

Тогда получим

\({I_z} = {I_{{z_C}}} + m{a^2}\) (5.8)

– момент инерции I_z тела относительно произвольной оси равен сумме момента инерции тела \({I_{{z_C}}}\) относительно параллельной ей оси z_C, проходящей через центр масс, и величины ma², где m – масса тела, a – расстояние между осями.

Пример 1. Момент инерции тонкого стержня (массы m и длины \(\ell \)) относительно оси, перпендикулярной стрежню и проходящей через его конец, равен

\(I = \frac{1}{{12}}m{\ell ^2} + m{\left( {\frac{\ell }{2}} \right)^2} = \frac{1}{3}m{\ell ^2}\). (5.9)