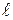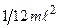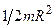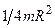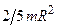Физика
1.1.9. Твердое тело. Поступательное и вращательное движение твердого тела
Момент инерции твердого тела
При изучении вращения твердых тел будем пользоваться понятием момента инерции.
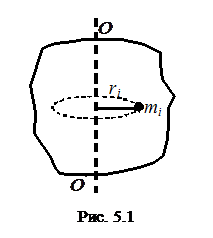 Разобьем тело на такие малые части, что каждую из них можно считать материальной точкой (рис. 5.1). Пусть mi – масса i-й материальной точки, ri – ее расстояние до некоторой оси OO'.
Разобьем тело на такие малые части, что каждую из них можно считать материальной точкой (рис. 5.1). Пусть mi – масса i-й материальной точки, ri – ее расстояние до некоторой оси OO'.
Величина, равная произведению массы материальной точки на квадрат кратчайшего расстояния ее до данной оси, называется моментом инерции материальной точки относительно оси:
\({I_i} = {m_i}r_i^2\). (5.1)
Сумма моментов инерции всех материальных точек тела называется моментом инерции тела относительно некоторой оси:
\(I = \sum\limits_{i = 1}^n {{m_i}} r_i^2\). (5.2)
Момент инерции твердого тела зависит, как нетрудно видеть, от распределения масс относительно интересующей нас оси.
Если тело представляет собой обруч массы m, толщина которого мала по сравнению с радиусом R, то момент его инерции относительно оси, проходящей через центр и перпендикулярной к плоскости обруча, равен
\(I = \sum\limits_i {{m_i}r_i^2} = \sum\limits_i {{m_i}} {R^2} = {R^2}\sum\limits_i {{m_i} = m{R^2}} \). (5.3)
Для тел более сложной формы суммирование выражения (5.2) производится методами интегрального исчисления согласно формуле
\(I = \int\limits_V {{r^2}{\rm{d}}m} \), (5.4)
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами x, y, z.
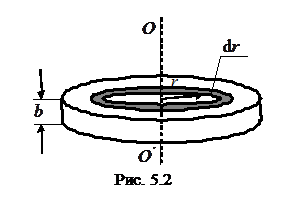 В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис. 5.2). Разобьем диск на кольцевые слои толщиной dr.
В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис. 5.2). Разобьем диск на кольцевые слои толщиной dr.
Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном r. Объем такого слоя равен
\({\rm{d}}V = b \cdot 2\pi {\rm{ }}r{\rm{ d}}r\),
где b – толщина диска. Поскольку диск однороден, плотность его 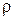 во всех точках одинакова и
во всех точках одинакова и
\({\rm{d}}m = \rho \cdot {\rm{ d}}V = 2\pi {\rm{ }}r{\rm{ }}b{\rm{ }}\rho {\rm{ d}}r\),
где dm – масса кольцевого слоя.
Теперь по формуле (5.4) находим момент инерции
\(I = \rho \int\limits_0^R {{r^2}{\rm{ }}} b{\rm{ }}2\pi {\rm{ }}r{\rm{ d}}r\),
где R – радиус диска;
\(I = 2\pi {\rm{ }}\rho {\rm{ }}b\int\limits_0^R {{r^3}{\rm{d}}r = 2\pi {\rm{ }}b{\rm{ }}\rho \frac{{{R^4}}}{4}} \).
Наконец, введя массу диска m, равную произведению плотности 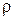 на объем диска
на объем диска 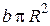 , получим
, получим
\(I = \frac{{m{R^2}}}{2}\). (5.5)
Моменты инерции некоторых однородных твердых тел относительно оси, проходящей через центр масс тела, приведены в табл. 5.1.
Таблица 5.1
| Твердое тело | Ось вращения | Момент инерции |
| Тонкий стержень длины | Перпендикулярна стержню |
|
| Сплошной цилиндр | Совпадает с осью цилиндра и проходит через центр тяжести |
|
| Тонкий диск радиуса R | Совпадает с диаметром диска |
|
| Шар радиуса R | Проходит через центр тяжести шара |
|
Другие материалы по данной теме
Видео
Поступательное и вращательное движения
Формула
\({a_\tau } = \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = R\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = R\varepsilon \)
Определение
Поступательное движение