Пусть тело вращается вокруг оси О под действием силы\(\vec F\)(рис. 5.6). Найдем работу этой силы.

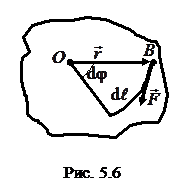При повороте тела на бесконечно малый угол \({\rm{d}}\phi \) точка приложения силы B проходит путь

\({\rm{d}}\ell = r \cdot {\rm{d}}\phi \),

где r – радиус окружности, описываемой точкой B. Элементарная работа равна

\({\rm{d}}A = F \cdot r \cdot {\rm{d}}\phi = F \cdot r \cdot \omega \cdot {\rm{d}}t\). (5.16)

Эта работа идет на увеличение кинетической энергии вращающегося тела. Так как \({E_{к\rm{}}} = \frac{{I{\omega ^2}}}{2}\), а \({\rm{d}}A = {\rm{d}}{E_{к\rm{}}}\), то

\({\rm{d}}{E_{к\rm{}}} = {\rm{d}}\left( {\frac{{I{\omega ^2}}}{2}} \right) = I{\rm{ }}\omega {\rm{ d}}\omega \). (5.17)

Поэтому \(F \cdot r \cdot \omega \cdot {\rm{d}}t = I{\rm{ }}\omega {\rm{ d}}\omega \).

Радиус окружности r является плечом силы F, следовательно, \(M = F \cdot r\) и

\(M{\rm{d}}t = I{\rm{d}}\omega \), (5.18)

или

\(M = I\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = I \cdot \varepsilon \). (5.19)

Учитывая, что векторы \(\vec M\) и \(\vec \varepsilon \) имеют одинаковое направление, придем к соотношению

\(\vec M = I\vec \varepsilon \). (5.20)

Это – основное уравнение динамики вращательного движения вокруг неподвижной оси. Оно напоминает второй закон Ньютона для поступательного движения. Роль массы играет момент инерции I, роль линейного ускорения – угловое ускорение \(\vec \varepsilon \), роль силы – момент силы \(\vec M\).

Из этого уравнения, в частности, видно, что момент инерции I определяет инерционные свойства тела при вращении: при одном и том же значении момента сил \(\vec M\) тело с большим моментом инерции приобретает меньшее угловое ускорение \(\vec \varepsilon \). Заметим, что работа при вращении тела согласно (5.16) равна \({\rm{d}}A = F \cdot r \cdot {\rm{d}}\phi = F \cdot r \cdot \omega \cdot {\rm{d}}t\). На рис. 5.6 сила \(\vec F \bot \vec r\), поэтому \(\vec M = \left[ {\vec r\vec F} \right]\) или \(M = F \cdot r\). С другой стороны, \({\rm{d}}\vec \phi = \vec \omega \cdot {\rm{d}}t\) – угловое перемещение. Векторы \(\vec M\) и \({\rm{d}}\vec \phi \) направлены по одной прямой, поэтому \({\rm{d}}A = (\vec M \cdot {\rm{d}}\vec \phi )\) или

\({\rm{d}}A = M \cdot {\rm{d}}\phi \) (5.21)

(сравним с формулой для работы при поступательном движении тела \({\rm{d}}A = (\vec F \cdot {\rm{d}}\vec r)\)).