Пример 2. Рассмотрим случай вращательного движения человека, находящегося на скамье Жуковского (рис. 6.10). Скамья Жуковского представляет собой горизонтальную платформу (диск), которая может свободно вращаться без трения вокруг вертикальной оси ОО₁. Человек сидит на скамье и держит в вытянутых руках гимнастические гантели и вращается вместе со скамьей вокруг оси ОО₁ с угловой скоростью \({\omega _1}\).

Если человек прижмет гантели к себе, то момент инерции системы уменьшится. Поскольку момент внешних сил (сил тяжести и реакции подшипников) относительно оси ОО₁ равен нулю, то момент импульса системы относительно оси ОО₁ сохраняется:

\(({I_0} + 2mr_1^2){\omega _1} = ({I_0} + 2mr_2^2){\omega _2}\),

где \({I_0}\) – момент инерции человека и скамьи относительно оси ОО₁; \(2mr_1^2\) и \(2mr_2^2\) – моменты инерции гантелей в первом и втором положениях относительно оси ОО₁; m – масса одной гантели; r₁ и r₂ – расстояния от гантелей до оси вращения; \({\omega _1}\;\) и \({\omega _2}\;\) – угловые скорости вращения системы. Очевидно, что если r₂ < r₁, то \({\omega _2}\;\) возрастает.

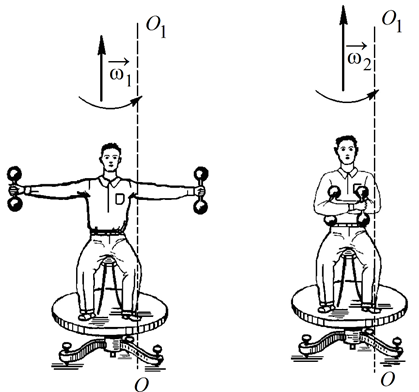
Рис. 6.10