Абсолютно неупругий удар – это удар, при котором часть механической энергии системы соударяющихся тел превращается в другие виды энергии.

Имеем шары массами m₁ и m₂, их скорости соответственно равны \({\vec v_1}\) и \({\vec v_2}\) (рис. 6.9). В момент удара шары деформируются, но эта деформация не исчезает и шары после удара двигаются с одинаковой скоростью.

Рис. 6.9

Найдем скорость шаров после удара. Закон сохранения импульса можно записать в проекции на направление движения:

\({m_1}{\rm{ }}{v_1} + {m_2}{\rm{ }}{v_2} = \left( {{m_1} + {m_2}} \right){\rm{ }}u\), (6.27)

где \(u\) – скорость шаров после удара. Тогда

\(u = \frac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}}\). (6.28)

Закон сохранения кинетической энергии при абсолютно неупругом ударе не выполняется. Часть кинетической энергии расходуется на работу деформации. Эту «потерю» можно определить по разности кинетической энергии тел до и после удара:

\(\Delta {E_{к\rm{}}} = \left( {\frac{{{m_1}v_1^2}}{2} + \frac{{{m_2}v_2^2}}{2}} \right) - \frac{{\left( {{m_1} + {m_2}} \right){\rm{ }}{u^2}}}{2}\). (6.29)

Используя (6.28), получим

\(\Delta {E_{к\rm{}}} = \frac{{{m_1}{m_2}}}{{2\left( {{m_1} + {m_2}} \right)}}{\left( {{v_1} - {v_2}} \right)^2}\). (6.30)

Эта часть кинетической энергии превращается в тепловую энергию, т.е. в энергию беспорядочного хаотического движения молекул. На практике часто приходится иметь дело со случаем, когда одно из тел (ударяемое тело) неподвижно, т.е. 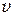= 0. В таком случае формула (6.30) имеет вид

\(\Delta {E_{к\rm{}}} = {E_1}\frac{{{m_2}}}{{{m_1} + {m_2}}}\), (6.31)

где \({E_1} = \frac{{{m_1}v_1^2}}{2}\) – кинетическая энергия ударяющегося тела.

Если целью удара является деформация тела (ковка, штамповка металла), необходимо, чтобы бόльшая часть энергии ударяющегося тела расходовалась на работу деформации, т.е. \(\Delta {E_{к\rm{}}}\) была по возможности больше. Для этого надо брать m₁<<m₂ (при ковке масса наковальни с куском металла много больше, чем масса молота). Если в результате удара необходимо получить перемещение неподвижного тела (забивание гвоздя), надо, чтобы потеря энергии на деформацию была наименьшей. Поэтому масса молотка должна быть гораздо больше массы гвоздя.