Рассмотрим материальную точку (тело), которая находится в консервативном силовом поле, ее скорость \(\vec v\), а потенциальная энергия задана функцией \(E_{\rm{п}}^{} = {E_{\rm{п}}}\left( {x,y,z} \right)\).

Полной механической энергией Е материальной точки называется сумма ее кинетической и потенциальной энергий:

\(E = {E_{\rm{к}}} + {E_{\rm{п}}} = \frac{{m{v^2}}}{2} + {E_{\rm{п}}}\). (4.35)

Сформулируем закон сохранения полной механической энергии материальной точки.

Если на материальную точку (тело) действуют только консервативные силы, ее полная механическая энергия с течением времени не изменяется (сохраняется):

\(E = {E_{\rm{к}}} + {E_{\rm{п}}} = \frac{{m{v^2}}}{2} + {E_{\rm{п}}} = {\rm{const}}\). (4.36)

Доказательство этого утверждения основано на теореме о кинетической энергии и свойствах консервативных сил. Пусть материальная точка переместилась из произвольного начального положения 1 в произвольное конечное положение 2 (из точки 1 в точку 2 пространства). Согласно теореме о кинетической энергии работа А_1-2 сил поля равна приращению кинетической энергии материальной точки:

\({A_{1 - 2}} = {E_{{\rm{к2}}}} - {E_{{\rm{к1}}}}\), (4.37)

где \({E_{{\rm{к}}2}}\) и \({E_{{\rm{к}}1}}\) – кинетическая энергия материальной точки в конечном и начальном положениях соответственно.

В процессе перемещения на материальную точку действуют только консервативные силы, работа которых равна убыли потенциальной энергии:

\({A_{1 - 2}} = {E_{{\rm{п}}1}} - {E_{{\rm{п}}2}}\),

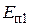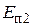где  и  – потенциальная энергия материальной частицы в начальном и конечном положениях соответственно.

Так как \({A_{1 - 2}} = {E_{{\rm{к}}2}} - {E_{{\rm{к}}1}}\) и \({A_{1 - 2}} = {E_{{\rm{п}}1}} - {E_{{\rm{п}}2}}\), то

\({E_{{\rm{к}}2}} - {E_{{\rm{к}}1}} = {E_{{\rm{п}}1}} - {E_{{\rm{п}}2}}\), или \({E_{{\rm{к}}2}} + {E_{{\rm{к}}2}} = {E_{{\rm{п}}1}} + {E_{{\rm{п}}1}}\), Е₂ = Е₁, (4.38)

где Е₂ и Е₁ – полная механическая энергия материальной точки в конечном и начальном положении соответственно.

Это выражение означает, что полная механическая энергия материальной точки в начальном положении равна полной механической энергии в конечном положении. Поскольку начальное и конечное положения выбраны произвольно, то можно утверждать, что полная механическая энергия материальной точки в процессе движения не изменяется (сохраняется).

Таким образом, если материальная точка находится в силовом поле, в котором действуют только консервативные силы, то полная механическая энергия материальной точки не изменяется со временем: \(E = {\rm{const}}\). Консервативные силы не могут изменить полную механическую энергию материальной точки в процессе движения.