Абсолютно упругий удар – это удар, при котором механическая энергия системы соударяющихся тел не превращается в другие виды энергии.

Пусть оба шара движутся вдоль оси x (рис. 6.4). Скорости шаров с массами m₁ и m₂ до удара – \({\vec v_1}\) и \({\vec v_2}\), после удара – \({\vec u_1}\) и \({\vec u_2}\).

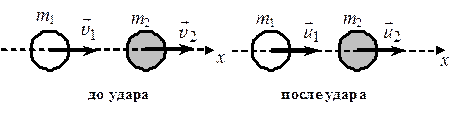
Рис. 6.4

Проекции векторов скорости на ось x равны модулям скоростей. В момент удара шары деформируются (сжимаются). В обоих шарах возникают упругие силы, которые стремятся восстановить форму шара. Эти силы замедляют движение первого шара и ускоряют движение второго. Так как удар абсолютно упругий, шары полностью восстанавливают свою форму, затем расходятся и движутся уже со скоростями, отличными

от скоростей до удара. При соударении в телах возникают столь значительные силы, что внешними силами, действующими на них, можно пренебречь и считать, что шары образуют замкнутую систему. Применим к шарам закон сохранения энергии и закон сохранения импульса.

По закону сохранения кинетической энергии

\(\frac{{{m_1}v_1^2}}{2} + \frac{{{m_2}v_2^2}}{2} = \frac{{{m_1}u_1^2}}{2} + \frac{{{m_2}u_2^2}}{2}\). (6.20)

Закон сохранения импульса (в проекциях на ось x):

\({m_1}{v_1} + {m_2}{v_2} = {m_1}{u_1} + {m_2}{u_2}\). (6.21)

Переносим в обоих равенствах члены с m₁ влево, с m₂ – вправо:

\(\begin{array}{l}{m_1}v_1^2 - {m_1}u_1^2 = {m_2}u_2^2 - {m_2}v_2^2;\\{m_1}{v_1} - {m_1}{u_1} = {m_2}{u_2} - {m_2}{v_2},\end{array}\) (6.22)

откуда

\({v_1} + {u_1} = {u_2} + {v_2}\). (6.23)

Решая совместно (6.20) и (6.21), находим скорости шаров после удара:

\({u_1} = \frac{{\left( {{m_1} - {m_2}} \right){\rm{ }}{v_1} + 2{m_2}{\rm{ }}{v_2}}}{{{m_1} + {m_2}}}\); (6.24)

\({u_2} = \frac{{\left( {{m_2} - {m_1}} \right){\rm{ }}{v_2} + 2{m_1}{v_1}}}{{{m_1} + {m_2}}}\). (6.25)