Рассмотрим материальную точку, положение которой может быть определено с помощью одной величины, например, координаты x, т.е. потенциальная энергия точки является функцией ${E_{п\rm{}}} = {E_{п\rm{}}}\left( x \right)$.

Графическая зависимость потенциальной энергии от координаты x называется потенциальной кривой. Зная вид функции E_п(x), можно сделать ряд заключений о характере движения частицы.

В качестве примера рассмотрим шарик, скользящий без трения по изогнутой в вертикальной плоскости проволоке. На шарик действует консервативная сила – сила тяжести. График потенциальной энергии E_п(x) показан на рис. 4.15. Проанализируем эту кривую. Полная энергия шарика E изображена на графике горизонтальной линией, поскольку имеет место закон сохранения энергии E = E_к+ E_п.

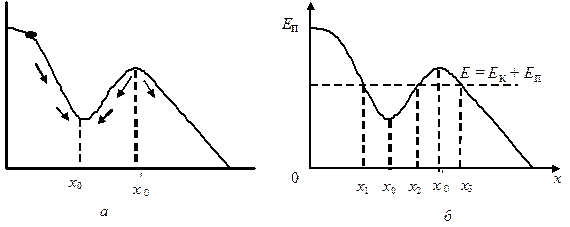
Рис. 4.15

Частица может находиться только там, где ${E_{п\rm{}}}\left( x \right) \le E$, т.е. в областях от x₁ до x₂ или от x₃ до бесконечности. В области x < x₁ и x₂< x < x₃ частица проникнуть не может, т.к. потенциальная энергия не может стать больше полной энергии. Таким образом, область x₂< x < x₃ представляет собой потенциальный барьер, через который частица не может проникнуть при данном запасе полной энергии. Область x₁ < x < x₂ называется потенциальной ямой.

Минимуму потенциальной энергии соответствует на графике точка с координатой x₀. Условие минимума потенциальной энергии имеет вид $\frac{{{\rm{d}}{E_{п\rm{}}}}}{{{\rm{d}}x}} = 0$.

Поскольку действующая на частицу сила

${F_x} = - \frac{{{\rm{d}}{E_{п\rm{}}}}}{{{\rm{d}}x}}$, (4.41)

то в точке x₀ ${F_x} = 0$. При смещении частицы из положения x₀ она испытывает действие возвращающей силы, поэтому положение x₀ является положением устойчивого равновесия. Итак, устойчивому равновесию соответствует минимум потенциальной энергии частицы. В точке ${x'_0}$, соответствующей максимуму потенциальной энергии, выполняются эти же условия равновесия. Однако это равновесие будет неустойчивым, т.к. при смещении частицы из положения ${x'_0}$ возникает сила, которая будет удалять его из положения равновесия.

Таким образом, неустойчивому равновесию соответствует максимум потенциальной энергии.

В точке х₀: $\frac{{{\rm{d}}{E_{\rm{p}}}}}{{{\rm{d}}x}} = {\rm{0}}$, следовательно сила равна нулю и тело находится в равновесии. Тело находится в положении устойчивого равновесия, если потенциальная энергия тела минимальная (рис. 4.16). Этот вывод распространяется и на систему тел.

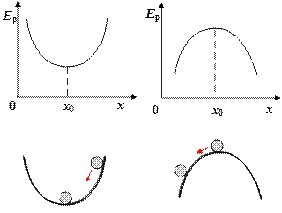
Рис. 4.16